TRIANGLE RECTANGLE - TRIGONOMETRIE
|
Exercice 1
1) Le triangle ABC est rectangle en A donc d'après le théorème de Pythagore :\[ \begin{align*} &AB^{2}+AC^{2}=BC^{2}\\ &AB^{2}=BC^{2}-AC^{2}\\ &AB^{2}=3.50^{2}-3.05^{2}\\ &AB^{2}=12.25-9.3025\\ &CD^{2}=2.9475\\ &CD=\sqrt{2.9475}\text{ mètres valeur exacte}\\ &CD \approx 1.72\text{ mètres valeur approchée} \end{align*} \] Il doit installer son échelle à environ 1.72 m du pied du mur.
2) Il s'agit de calculer la mesure de l'angle \(\widehat{ABC}\). Le triangle ABC étant rectangle en A, on a :
\[ \begin{align*} \sin{\widehat{ABC}}&=\frac{\text{côté opposé à }\widehat{ABC}}{\text{hypoténuse}}\\ &=\frac{AC}{BC}\\ &=\frac{3.05}{3.5}\\ &\approx 0.871 \end{align*} \] En utilisant la calculatrice et la touche sin-1, on obtient \(\widehat{ABC}\approx 60.58^{\circ}\).
Exercice 2
1) Le triangle ABC est rectangle en B et on souhaite connaître la longueur AB. On peut utiliser la tangente de l'angle \(\widehat{BAC}\). Nous avons d'une part :\[ \begin{align*} \tan{\widehat{BAC}}&=\frac{\text{côté opposé à }\widehat{BAC}}{\text{côté adjacent à }\widehat{BAC}}\\ &=\frac{BC}{AB}\\ &=\frac{324}{AB} \end{align*} \] Et d'autre part :
\[ \tan{\widehat{BAC}}=\tan(30) \] On peut en déduire l'égalité suivante :
\[ \begin{align*} &\tan(30)=\frac{324}{AB}\\ \Rightarrow & AB=\frac{324}{\tan(30)}\\ & AB \approx 561.18\text{ mètres valeur approchée} \end{align*} \] Il devra se situer à environ 561.18 mètres de la Tour Eiffel pour pouvoir l'admirer sans mal.
2) On calcule la tangente de l'angle \(\widehat{BAC}\) sachant que BA = 700 mètres :
\[ \begin{align*} \tan{\widehat{BAC}}&=\frac{\text{côté opposé à }\widehat{BAC}}{\text{côté adjacent à }\widehat{BAC}}\\ &=\frac{BC}{AB}\\ &=\frac{324}{700}\\ &\approx 0.463 \end{align*} \] En utilisant la calculatrice et la touche tan-1, on obtient \(\widehat{BAC}\approx 24.84^{\circ}\).
Exercice 3
Rappel de la figure :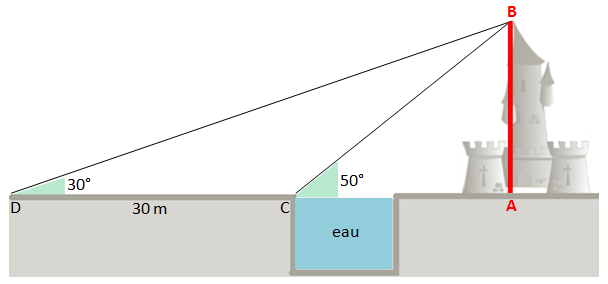
Le triangle ABC est en effet rectangle en A donc :
\[ \begin{align*} \tan{\widehat{ACB}}&=\frac{\text{côté opposé à }\widehat{ACB}}{\text{côté adjacent à }\widehat{ACB}}\\ &=\frac{AB}{AC}\\ &=\tan(50) \end{align*} \] Nous pouvons donc écrire AB de la façon suivante :
\[AB=\tan(50)\times AC\text{ (1)} \] Le triangle ABD est aussi rectangle en A :
\[ \begin{align*} \tan{\widehat{ADB}}&=\frac{\text{côté opposé à }\widehat{ADB}}{\text{côté adjacent à }\widehat{ADB}}\\ &=\frac{AB}{AD}\\ &=\frac{AB}{AC+CD}\\ &=\frac{AB}{AC+30}\\ &=\tan(30) \end{align*} \] Nous pouvons donc réécrire AB de la façon suivante :
\[\tan(30)\times (AC+30)=AB\text{ (2)}\] A partir des relations (1) et (2), nous pouvons écrire :
\[\tan(50)\times AC=\tan(30)\times (AC+30)\] Nous pouvons à présent trouver la longueur AC :
\[ \begin{align*} &\tan(50)\times AC=\tan(30)\times (AC+30)\\ \Leftrightarrow & \tan(50)\times AC=\tan(30)\times AC+30\tan(30)\\ \Leftrightarrow & \tan(50)\times AC-\tan(30)\times AC=30\tan(30)\\ \Leftrightarrow & (\tan(50)-\tan(30))\times AC=30\tan(30)\\ \Leftrightarrow & AC=\frac{30\tan(30)}{\tan(50)-\tan(30)}\\ \Leftrightarrow & AC\approx 28.19\text{ mètres} \end{align*} \] AC mesure environ 28.19 mètres. Pour déterminer AB, on remplace AC dans la relation (1) par exemple :
\[ \begin{align*} AB&=\tan(50)\times AC\\ &\approx \tan(50)\times 28.19\\ &\approx 33.6 \text{ mètres} \end{align*} \] La hauteur du chateau est de 33.6 mètres.