PROBABILITES
|
Exercice 1 (France juin 2009)
1) La probabilité se calcule en divisant le nombre de billes rouges dans un sac par le nombre total de billes.\[ P=\frac{\text{Nombre de billes rouges}}{\text{Nombre total de billes}} \] Probabilité pour Aline de tirer une bille rouge :
\[ \frac{5}{5}=1 \] Probabilité pour Bernard de tirer une bille rouge :
\[ \frac{10}{30+10}=\frac{10}{40}=0.25 \] Probabilité pour Claude de tirer une bille rouge :
\[ \frac{100}{100+3}=\frac{100}{103}\approx 0.97 \] Aline a la plus forte probabilité de tirer une bille rouge.
2) La probabilité de Bernard de tirer une bille rouge est de 0,25 donc P = 0,25. Le nombre de billes rouges est de 5.
\[ \begin{align*} &P=\frac{\text{Nombre de billes rouges}}{\text{Nombre total de billes}}\\ &0.25=\frac{5}{\text{Nombre total de billes}}\\ &\text{Nombre total de billes}=\frac{5}{25}\\ &\text{Nombre total de billes}=20 \end{align*} \] Le nombre total de billes est de 20 donc le nombre de billes noires est égal à \(20-5=15\).
Il faut ajouter 15 billes noires à Aline pour qu’elle ait la même probabilité que Bernard de tirer une bille rouge.
Exercice 2 (Pondichéry avril 2009)
1) Il y a 6 boules dont 4 blanches.La probabilité de tirer une boule blanche, notée ici \(P(A)\) est égale à
\[ \begin{align*} P(A)&=\frac{\text{Nombre de boules blanches}}{\text{Nombre total de boules}}\\ &=\frac{4}{6}\\ &=\frac{2}{3}\\ \end{align*} \] La réponse A est la bonne.
2) Il y a 6 boules dont 2 portant le numéro 2.
La probabilité de tirer une boule portant le numéro 2, notée ici \(P(B)\) est égale à
\[ \begin{align*} P(B)&=\frac{\text{Nombre de boules numérotées 2}}{\text{Nombre total de boules}}\\ &=\frac{2}{6}\\ &=\frac{1}{3}\\ \end{align*} \] La réponse C est la bonne.
3) Il y a 6 boules dont 2 blanches portant le numéro 1.
La probabilité de tirer une boule blanche portant le numéro 1, notée ici \(P(C)\) est égale à
\[ \begin{align*} P(C)&=\frac{\text{Nombre de boules blanches numérotées 1}}{\text{Nombre total de boules}}\\ &=\frac{2}{6}\\ &=\frac{1}{3}\\ \end{align*} \] La réponse A est la bonne.
Exercice 3 (Polynésie juin 2009)
La roue comporte 8 secteurs. Chaque secteur a autant de chance d’être désigné.1) Un seul secteur permet de gagner un autocollant
\[ P(A)=\frac{1}{8}=0.125 \] La probabilité de gagner un autocollant est de 0,125.
2) Quatre secteurs permettent de gagner un T-shirt
\[ P(T)=\frac{4}{8}=\frac{1}{2}=0.5 \] La probabilité de gagner un T-shirt est de 0,5.
3) Trois secteurs permettent de gagner un tour de manège.
\[ P(M)=\frac{3}{8}=0.375 \] La probabilité de gagner un tour de manège est de 0,375.
4) L’évènement « non \(A\) » consiste à ne pas gagner un autocollant.
\[ \begin{align*} P(\overline{A})&=1-P(A)\\ &=1-\frac{1}{8}\\ &=\frac{7}{8}\\ &=0.875 \end{align*} \] La probabilité de ne pas gagner un autocollant est de 0,875.
Exercice 4 (Polynésie juin 2014)
1) Nombre total de boules dans le sac :\(3 + 5 + 2 + 2 + 2 + 6 = 20\).
Il y a 20 boules dans le sac.
2) On tire une boule au hasard, on note sa couleur et sa lettre.
a) Nombre de boules bleues
portant la lettre A : \(2\)
Nombre total de boules dans le sac : \(20\)
La probabilité d'avoir une boule bleue avec la lettre A est égale à :
\[ p=\frac{2}{20}=\frac{1}{10}=0.1 \] On a bien une chance sur 10 d'avoir une boule bleue avec la lettre A.
b) Le nombre total de boules rouges est égal au nombre de boules rouges avec la lettre A additionné au nombre de boules rouges avec la lettre B :
\(3 + 2 = 5\)
Nombre total de boules dans le sac : \(20\)
La probabilité d'avoir une boule rouge dans le sac est égale à :
\[ p=\frac{5}{20}=\frac{1}{4}=0.25 \] On a une chance sur 4, c'est-à-dire une probabilité de 0.25 de tirer une boule rouge.
c) Nombre de boules avec la lettre A : \(3 + 5 + 2 = 10\)
Nombre de boules avec la lettre B : \(2 + 2 + 6 = 10\)
Nombre total de boules dans le sac : \(20\)
Ici, la probabilité de tirer une boule avec la lettre A ou une boule avec la lettre B est identique et égale à :
\[ p=\frac{10}{20}=\frac{1}{2}=0.5 \] On a autant de chance de tirer une boule avec la lettre A qu'une boule avec la lettre B (une chance sur deux).
Nombre total de boules dans le sac : \(20\)
La probabilité d'avoir une boule bleue avec la lettre A est égale à :
\[ p=\frac{2}{20}=\frac{1}{10}=0.1 \] On a bien une chance sur 10 d'avoir une boule bleue avec la lettre A.
b) Le nombre total de boules rouges est égal au nombre de boules rouges avec la lettre A additionné au nombre de boules rouges avec la lettre B :
\(3 + 2 = 5\)
Nombre total de boules dans le sac : \(20\)
La probabilité d'avoir une boule rouge dans le sac est égale à :
\[ p=\frac{5}{20}=\frac{1}{4}=0.25 \] On a une chance sur 4, c'est-à-dire une probabilité de 0.25 de tirer une boule rouge.
c) Nombre de boules avec la lettre A : \(3 + 5 + 2 = 10\)
Nombre de boules avec la lettre B : \(2 + 2 + 6 = 10\)
Nombre total de boules dans le sac : \(20\)
Ici, la probabilité de tirer une boule avec la lettre A ou une boule avec la lettre B est identique et égale à :
\[ p=\frac{10}{20}=\frac{1}{2}=0.5 \] On a autant de chance de tirer une boule avec la lettre A qu'une boule avec la lettre B (une chance sur deux).
Exercice 5 (France septembre 2014)
1) Si l’infirmière en ramasse une au hasard, quelle est la probabilité que cette fiche soit :a) Nombre total d'élèves
de la classe :
\(3 + 15 + 7 + 5 = 30\)
Nombre de filles portant des lunettes : \(3\)
La probabilité que la fiche soit celle d'une fille portant des lunettes est égale à :
\[ p=\frac{3}{30}=\frac{1}{10}=0.1 \] Il y a une chance sur dix pour que la fiche soit celle d'une fille qui porte des lunettes.
b) Nombre de garçons : \(7 + 5 = 12\)
Nombre total d'élèves de la classe : \(30\)
La probabilité que la fiche soit celle d'un garçon est égale à :
\[ p=\frac{12}{30}=\frac{4}{10}=0.4 \] La probabilité que la fiche soit celle d'un garçon est égale à 0,4.
\(3 + 15 + 7 + 5 = 30\)
Nombre de filles portant des lunettes : \(3\)
La probabilité que la fiche soit celle d'une fille portant des lunettes est égale à :
\[ p=\frac{3}{30}=\frac{1}{10}=0.1 \] Il y a une chance sur dix pour que la fiche soit celle d'une fille qui porte des lunettes.
b) Nombre de garçons : \(7 + 5 = 12\)
Nombre total d'élèves de la classe : \(30\)
La probabilité que la fiche soit celle d'un garçon est égale à :
\[ p=\frac{12}{30}=\frac{4}{10}=0.4 \] La probabilité que la fiche soit celle d'un garçon est égale à 0,4.
2) Nombre d'élèves portant des lunettes dans cette classe : \(3+ 7 = 10\)
Leur proportion est de 12.5%, c'est-à-dire que parmi les élèves portant des lunettes dans ce collège, la probabilité qu'ils appartiennent à cette classe est égale à 0.125.
Soit \(x\) le nombre d'élèves qui portent des lunettes dans ce collège.
\[ \begin{align*} &\frac{10}{x}=0.125\\ &x=\frac{10}{0.125}=80 \end{align*} \] 80 élèves portent des lunettes dans ce collège.
Exercice 6 (Polynésie septembre 2014)
1) Non, on ne peut pas affirmer que cette bouteille contient exactement 9 billes rouges, 4 billes bleues et 7 billes vertes. En effet, étant donné que la bille reste dans la bouteille, une même bille peut apparaître au goulot à maintes reprises et donc être comptabilisée plusieurs fois. Pour connaitre le nombre de billes de chaque couleur, il aurait fallu à chaque tirage enlever la bille de la bouteille jusqu'à ce que celle-ci soit vide.2) Nombre de billes vertes :
\[ \frac{3}{8}\times 24=9 \] Il y a 9 billes vertes dans la bouteille.
Nombre de biles bleues :
\[ \frac{1}{2}\times 24=12 \] Il y a 12 billes bleues dans la bouteille.
Nombre de billes rouges : \(24 - 9 - 12 = 3\)
Il y a 3 billes rouges dans la bouteille.
Exercice 7 (Nouvelle-Calédonie décembre 2014)
1)a) Je gagne si
l'adversaire joue
ciseaux, je fais match nul si l'adversaire joue pierre, et je perds si
l'adversaire joue feuille. Il y a donc 3 cas possibles et je
perds dans un cas sur 3. La probabilité de perdre est ici égale
à \(\displaystyle \frac{1}{3}\).
b) "Ne pas perdre" est l'évènement contraire de "perdre". Par conséquent, "ne pas perdre" se produit avec une probabilité égale à : \[ 1-\frac{1}{3}=\frac{2}{3} \] On a deux chances sur trois de ne pas perdre la partie (c'est-à-dire de faire match nul ou de gagner).
b) "Ne pas perdre" est l'évènement contraire de "perdre". Par conséquent, "ne pas perdre" se produit avec une probabilité égale à : \[ 1-\frac{1}{3}=\frac{2}{3} \] On a deux chances sur trois de ne pas perdre la partie (c'est-à-dire de faire match nul ou de gagner).
2) Je joue deux parties de suite et je choisis de jouer «pierre» à chaque partie.
Mon adversaire joue au hasard.
Construire l’arbre des possibles de l’adversaire pour ces deux parties. On notera P, F, C, pour pierre, feuille, ciseaux.
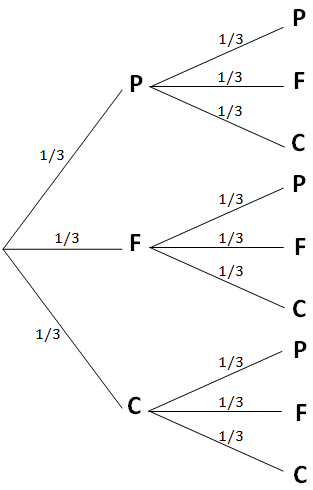
3)
a) Je
gagne les deux parties si l'adversaire joue "ciseaux" puis "ciseaux".
Il s'agit du chemin (C,C) sur l'arbre de jeu. La probabilité que je
gagne les deux parties en jouant "ciseaux" à chaque fois est égale à :
\[ p=\frac{1}{3}\times \frac{1}{3}=\frac{1}{9} \]
b) Je ne perds pas si je fais match nul ou si je gagne. Si je joue "pierre" à chaque fois, il faut que l'adversaire joue "pierre" (match nul) ou "ciseaux" (je gagne). Il y a quatre possibilités : (P,P), (P,C), (C,P), (C,C). Chacune de ces issues se produisent avec une probabilité égale à \(\displaystyle \frac{1}{9}\).
Par conséquent, la probabilité de ne pas perdre est égale à :
\[ 4\times \frac{1}{9}=\frac{4}{9} \]
\[ p=\frac{1}{3}\times \frac{1}{3}=\frac{1}{9} \]
b) Je ne perds pas si je fais match nul ou si je gagne. Si je joue "pierre" à chaque fois, il faut que l'adversaire joue "pierre" (match nul) ou "ciseaux" (je gagne). Il y a quatre possibilités : (P,P), (P,C), (C,P), (C,C). Chacune de ces issues se produisent avec une probabilité égale à \(\displaystyle \frac{1}{9}\).
Par conséquent, la probabilité de ne pas perdre est égale à :
\[ 4\times \frac{1}{9}=\frac{4}{9} \]
Exercice 8 (Nouvelle-Calédonie mars 2015)
1) Nombre de possibilités d'avoir un ballon : \(1\)Nombre de possibilités d'avoir un cadeau : \(6\)
La probabilité que Gilda gagne un ballon est égale à :
\[ p=\frac{1}{6} \] Gilda a une chance sur six de gagner un ballon.
2) Nombre de possibilités d'avoir une sucrerie : \(3\) (chocolat, sucettes, bonbons).
Nombre de possibilités d'avoir un cadeau : \(6\)
La probabilité que Marie gagne une sucrerie est égale à : \[ p=\frac{3}{6}=\frac{1}{2}=0.5 \] Marie a une chance sur deux de gagner une sucrerie.
3) De même qu'à la question 1, la probabilité de gagner du chocolat est égale à \(\displaystyle \frac{1}{6}\). La probabilité de gagner une petite voiture est aussi de \(\displaystyle \frac{1}{6}\). Par conséquent, pour obtenir la probabilité de gagner du chocolat puis une petite voiture, on doit multiplier ces deux probabilités : \[ p=\frac{1}{6}\times \frac{1}{6}=\frac{1}{36} \] Roméo a une chance sur 36 de gagner du chocolat puis une petite voiture.
Indication : Si vous avez des difficultés à obtenir ou à comprendre ce résultat, vous pouvez construire l'arbre du jeu. Comme vu dans le cours, on effectue le produit des probabilités inscrites sur les branches (chocolat, voiture) pour obtenir la probabilité voulue.