PROBABILITES
Cours

I) Définitions

A) L'expérience aléatoire

Définition
Une expérience aléatoire est une expérience dont le résultat ne peut pas être prédit de façon certaine car il est déterminé par le hasard.
Une issue ou éventualité est un résultat possible de cette expérience.


Exemple 1 :
Lorsqu'on lance un dé à 6 faces, on ne peut pas prédire de façon certaine quelle face va s'afficher.
Cette expérience aléaoire à 6 issues (ou éventualités) : obtenir 1, obtenir 2, obtenir 3, obtenir 4, obtenir 5, et obtenir 6.

B) Les évènements

Définition
Un évènement est un ensemble d'issues ou éventualités.

Exemple 2 :
On lance un dé à 6 faces. On appelle \(A\) l'évènement "obtenir un multiple de 2".
Les issues correspondant à cet évènement sont : obtenir 2, obtenir 4 et obtenir 6. Il y a donc 3 éventualités correspondant à cet évènement.

Définition
Un évènement élémentaire est un évènement composé d'une seule issue.


Exemple 3 :
Lors du lancer d'un dé à 6 faces, l'évènement "obtenir un multiple de 5" est un évènement élémentaire : la seule issue possible est d'obtenir 5.
Au contraire, l'évènement "obtenir un multiple de 3" n'est pas élémentaire : il y a en effet deux issues possibles (obtenir 3 et obtenir 6).

Définition
On appelle évènement contraire de \(A\) l'ensemble des éventualités qui ne sont pas dans \(A\).


Exemple 4 :
Soit B l'évènement "obtenir 6" au lancer de dé. L'évènement contraire est "ne pas obtenir 6".

Définition
On dit de deux évènements qu'ils sont incompatibles s'il n'est pas possible qu'ils se produisent en même temps.


Exemple 5 :
Lors du lancer de dé, l'évènement \(A\) "obtenir un nombre pair" et l'évènement \(B\) "obtenir un nombre impair" sont incompatibles : un nombre ne peut pas être à la fois pair et impair.

Définition
Un évènement est dit impossible s'il ne peut pas se produire. Il est dit certain s'il se produit nécessairement.


Exemple 6 :
Lorsqu'on effectue un seul lancer de dé, l'évènement "obtenir 11" est impossible.
L'évènement "obtenir plus de 0" est au contraire un évènement certain.



II) Notion de probabilité

Définition

Lorsqu'on répète un très grand nombre de fois une expérience aléatoire, la fréquence de réalisation d'un évènement \(A\) se rapproche d'une valeur particulière, appelée probabilité de l'évènement \(A\) et que l'on note \(P(A)\).



Exemple 7 :
La probabilité d'obtenir "Face" au lancer de pièce de monnaie est égale à 0.5 ou \(\displaystyle \frac{1}{2}\) : en effet, on a une chance sur deux que la pièce tombe sur "Face".
Sur un jeu de lancer de dé, appelons A l'évènement "Obtenir 5". Cet évènement se produit avec la probabilité \(\displaystyle \frac{1}{6}\) : nous avons une chance sur 6 que le dé tombe sur "5". Nous notons ainsi : \[ p(A)=\frac{1}{6} \]
Propriétés
Une probabilité est toujours un nombre compris entre 0 et 1 :
\(0\leq P(A) \leq 1\)

Un évènement dont la probabilité est égale à 1 est appelé évènement certain.
Un évènement impossible est un évènement dont la probabilité est égale à 0.
La somme des probabilités de tous les évènements élémentaires est toujours égale à 1.

Exemple 8 :
En reprenant l'exemple 6 (lancer de dé), la probabilité d'"obtenir 11" est égale à 0, car c'est un évènement impossible.
La probabilité d'"obtenir plus de 0" est quant à elle égale à 1, car c'est un évènement certain.
Pour le lancer de pièce de monnaie, la somme des probabilités d'obtenir "pile" et d'obtenir "face" est bien égale à 1.

Définition
Lorsque tous les évènements ont la même probabilité, on dit qu'ils sont équiprobables ou qu'il y a équiprobabilité. Dans une telle situation, si une expérience aléatoire possède \(n\) issues, alors la probabilité d'un évènement élémentaire est égale à l'inverse de \(n\) : \(\displaystyle \frac{1}{n}\)

Exemple 9 :
Le lancer de pièce et le lancer de dé sont deux jeux dont les issues sont équiprobables.
Il y a deux issues pour le lancer de pièce, la probabilité de chaque évènement est égale à \(\displaystyle \frac{1}{2}\).
Il y a six issues pour le lancer de dé, la probabilité de chaque évènement est égale à \(\displaystyle \frac{1}{6}\).

Définition
La somme des probabilités d'un évènement \(A\) et de son évènement contraire \(\overline{A}\) est égale à 1 :
\(P(A)+P(\overline{A})=1\)


III) Expériences aléatoires à deux épreuves

Exemple 10 :
On lance une pièce de monnaie et on note si on obtient "pile" ou "face". Si on obtient "face", le jeu est terminé et on n'a pas de gain (0€). Si on obtient "pile", on a le droit de tourner la roue suivante pour obtenir un gain de 100, 200 ou 500€ :


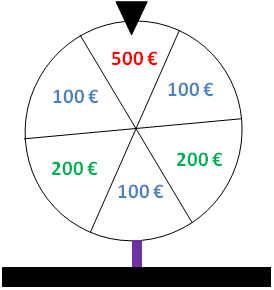
Il y a une seule possibilité d'avoir 500€, deux possibilités d'avoir 200€ et trois possibilités d'avoir 100€.
Notons les évènements suivants :
"P" : obtenir pile
"F" : obtenir face
"0€" : gagner 0€
"100€" : gagner 100€
"200€" : gagner 200€
"500€" : gagner 500€

On peut représenter ce jeu sous la forme d'un arbre : celui-ci permet de lire le déroulé du jeu, les différents évènements, les probabilités associées ainsi que les gains :


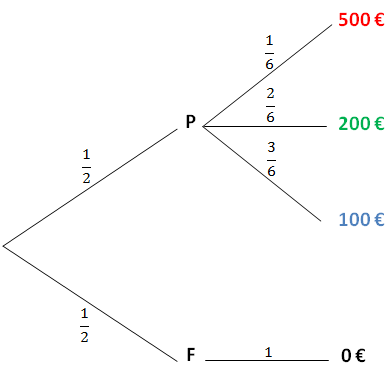
Lorsqu'on obtient "face", on a nécessairement 0€ : ainsi, obtenir "0€" est un évènement certain lorsqu'on a obtenu "face" au lancer de pièce.
Lorsqu'on obtient "pile", on a 1 chance sur 6 d'avoir 500€, 2 chances sur 6 d'avoir 200€ et 3 chances sur 6 d'avoir 100€.

Propriétés
Dans un arbre de jeu, la probabilité d'une issue est égale au produit des probabilités des branches conduisant à cette issue.

Dans l'exemple ci-dessus, calculons la probabilité d'obtenir 0€ :
\[\frac{1}{2}\times 1=\frac{1}{2}\] La probabilité de gagner 100€ est égale à :
\[\frac{1}{2}\times \frac{3}{6}=\frac{3}{12}\] La probabilité de gagner 200€ est égale à :
\[\frac{1}{2}\times \frac{2}{6}=\frac{2}{12}\] La probabilité de gagner 500€ est égale à :
\[\frac{1}{2}\times \frac{1}{6}=\frac{1}{12}\]
Cours sur les probabilités pour la troisième (3ème)
© Planète Maths