THEOREME DE THALES
Correction des exercices *

Exercice 1

Nous avons :
\(\displaystyle \frac{SA}{SR}=\frac{SB}{ST}=\frac{AB}{RT}\)
\(\displaystyle \frac{ZY}{ZV}=\frac{ZX}{ZU}=\frac{XY}{UV}\)
\(\displaystyle \frac{OM}{OP}=\frac{ON}{OQ}=\frac{MN}{PQ}\)

Exercice 2

Nous avons :
\(\displaystyle \frac{LI}{LH}=\frac{LJ}{LK}=\frac{IJ}{KH}\)
\(\displaystyle \frac{UY}{UV}=\frac{UX}{UW}=\frac{XY}{VW}\)

Exercice 3

Dans le triangle ABC, D est un point appartenant au segment [AC] et E un point appartenant au segment [BC]. De plus, les droites (AB) et (DE) sont parallèles donc d'après le théorème de Thalès, nous avons :
\[ \frac{CD}{CA}=\frac{CE}{CB}=\frac{DE}{AB} \] En remplaçant par les longueurs connues :
\[ \frac{3}{8}=\frac{4}{CB}=\frac{DE}{9} \]
1) Calcul de la longueur BC.
D'après ce que l'on a écrit précédemment, nous avons :
\[ \frac{3}{8}=\frac{4}{CB} \] On peut en déduire la longueur BC :
\[ \begin{align*} &\frac{3}{8}=\frac{4}{CB}\\ &CB=\frac{4\times 8}{3}\\ &CB=\frac{32}{3}\\ &BC\approx 10.67 \text{ cm} \end{align*} \] BC mesure approximativement 10.67 cm.

2) Calcul de la longueur DE.
D'après ce que l'on a écrit au début, nous avons :
\[ \frac{3}{8}=\frac{DE}{9} \] On peut en déduire la longueur DE :

\begin{align*}
&\frac{3}{8}=\frac{DE}{9}\\
&DE=\frac{3\times 9}{8}\\
&DE=\frac{27}{8}\\
&DE=3.375\text{ cm}
\end{align*}

DE mesure 3.375 cm.

Exercice 4

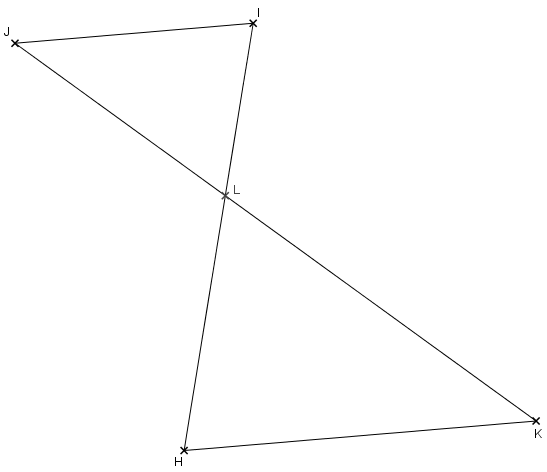
Les points J, L, K d'une part et les points I, L, H d'autre part sont alignés dans le même ordre. De plus, les droites (JI) et (HK) sont parallèles donc d'après le théorème de Thalès, nous avons :
\[ \frac{LI}{LH}=\frac{LJ}{LK}=\frac{IJ}{KH} \] En remplaçant par les longueurs connues :
\[ \frac{2.5}{5}=\frac{4}{LK}=\frac{IJ}{7} \]
1) Calcul de la longueur LK.
D'après ce que l'on a écrit précédemment, nous avons :
\[ \frac{2.5}{5}=\frac{4}{LK} \] On peut en déduire la longueur LK :
\[ \begin{align*} &\frac{2.5}{5}=\frac{4}{LK}\\ &LK=\frac{4\times 5}{2.5}\\ &LK=\frac{20}{2.5}\\ &LK=8 \text{ cm} \end{align*} \] KL mesure 8 cm.

2) Calcul de la longueur IJ.
D'après ce que l'on a écrit au début, nous avons :
\[ \frac{2.5}{5}=\frac{IJ}{7} \] On peut en déduire la longueur IJ :
\[ \begin{align*} &\frac{2.5}{5}=\frac{IJ}{7}\\ &IJ=\frac{2.5\times 7}{5}\\ &IJ=\frac{17.5}{5}\\ &IJ=3.5\text{ cm} \end{align*} \] IJ mesure 3.5 cm.

Exercice 5

Les points A, O, C d'une part et les points B, O, D d'autre part sont alignés dans le même ordre. De plus, nous avons :
\[ \begin{align*} &\frac{OB}{OD}=\frac{8}{16}=0.5\\ &\frac{OA}{OC}=\frac{5}{10}=0.5\\ \end{align*} \] Nous pouvons remarquer que :
\[ \frac{OB}{OD}=\frac{OA}{OC} \] Donc d'après la réciproque du théorème de Thalès, les droites (AB) et (CD) sont parallèles.

Exercice 6

Les points K, O, J d'une part et les points L, O, I d'autre part sont alignés dans le même ordre. De plus, nous avons :
\[ \begin{align*} &\frac{OJ}{OK}=\frac{2.7}{9}=0.3\\ &\frac{OI}{OL}=\frac{3}{12}=0.25\\ \end{align*} \] Nous pouvons remarquer que :
\[ \frac{OJ}{OK}\neq\frac{OI}{OL} \] Donc d'après la contraposée du théorème de Thalès, les droites (IJ) et (KL) ne sont pas parallèles.