TRIANGLE RECTANGLE - TRIGONOMETRIE
|
Exercice 1 (Amérique du Nord juin 2009)
1) Le triangle CDB est rectangle en D.\[ \begin{align*} \cos{\widehat{DBC}}&=\frac{\text{côté adjacent à }\widehat{DBC}}{\text{hypoténuse}}\\ &=\frac{BD}{BC} \end{align*} \] Donc : \[ \begin{align*} BC&=\frac{BD}{\cos{\widehat{DBC}}}\\ &=\frac{4}{\cos(60)}\\ &=\frac{4}{0.5}\\ &=8\text{ cm} \end{align*} \] BC mesure 8 cm.
2) Le triangle CBD est rectangle en D, on peut donc utiliser le théorème de Pythagore et écrire l’égalité suivante :
\[ \begin{align*} &CD^{2}+BD^{2}=BC^{2}\\ &CD^{2}=BC^{2}-BD^{2}\\ &CD^{2}=8^{2}-4^{2}\\ &CD^{2}=64-16\\ &CD^{2}=48\\ &CD=\sqrt{48}=\sqrt{16}\times \sqrt{3}=4\sqrt{3} \text{ valeur exacte}\\ &CD \approx 6.9\text{ cm valeur approchée}
\end{align*} \] CD mesure 6,9 cm.
(On pouvait également utiliser la tangente de l’angle\( \widehat{DBC}\).)
3) Le triangle ABC est rectangle en B, on peut donc utiliser le théorème de Pythagore et écrire l’égalité suivante :
\[ \begin{align*} &AB^{2}+BC^{2}=AC^{2}\\ &AC^{2}=6^{2}+8^{2}\\ &AC^{2}=36+64\\ &AC^{2}=100\\ &AC=\sqrt{100}\\ &AC=10\text{ cm} \end{align*} \] AC mesure 10 cm.
4) Le triangle ABC est rectangle en B.
\[ \begin{align*} \tan{\widehat{BAC}}&=\frac{\text{côté opposé à }\widehat{BAC}}{\text{côté adjacent à }\widehat{BAC}}\\ &=\frac{BC}{AB}\\ &=\frac{8}{6}\\ &=\frac{4}{3} \end{align*} \]
5) D’après la calculatrice et la touche tan-1, \(\widehat{BAC}\) mesure 53° (arrondi au degré près).
Exercice 2 (Centres étrangers juin 2009)
1) Figure2) [AB] est un diamètre du cercle \(\mathcal{C}\) et M un point de ce cercle donc le triangle ABM est rectangle en M.
3) Le triangle ABM est rectangle en M ; on peut donc utiliser les formules trigonométriques.
\[ \begin{align*} \cos{\widehat{ABM}}&=\frac{\text{côté adjacent à }\widehat{ABM}}{\text{hypoténuse}}\\ &=\frac{BM}{AB}\\ &=\frac{4.2}{10}\\ &=0.42 \end{align*} \] D’après la calculatrice, \(\widehat{ABM}\) mesure 65° (arrondi au degré près).
L’angle au centre \(\widehat{AOM}\) intercepte le même arc que l’angle inscrit \(\widehat{ABM}\) donc la mesure de l’angle \(\widehat{AOM}\) est le double de celle de l’angle \(\widehat{ABM}\).
\[ \begin{align*} \widehat{AOM}&=2\times \widehat{ABM}\\ &=2\times 65\\ &=130^{\circ} \text{ (au degré près)} \end{align*} \]
Exercice 3 (Liban juin 2009)
1) Figure en vraie grandeurABCD est un carré donc AD = AB = 4 cm.
\[ \begin{align*} &AM^{2}+MD^{2}=2.4^{2}+3.2^{2}=5.76+10.24=16\\ &AD^{2}=4^{2}=16 \end{align*} \] On a \(AM^{2}+MD^{2}=AD^{2}\) donc d’après la réciproque du théorème de Pythagore, le triangle AMD est rectangle en M.
3) Calcul de la mesure de l’angle \(\widehat{DAM}\)
\[ \begin{align*} \cos \widehat{DAM}&=\frac{\text{côté adjacent à }\widehat{DAM}}{\text{hypoténuse}}\\ &=\frac{AM}{AD}\\ &=\frac{2.4}{4}\\ &=0.6 \end{align*} \] D’après la calculatrice et la touche cos-1, \(\widehat{DAM}\approx 53^{\circ}\) (arrondi au degré près).
4) Le triangle ADI est rectangle en D donc
\[ \begin{align*} \tan{\widehat{DAI}}&=\frac{\text{côté opposé à }\widehat{DAI}}{\text{côté adjacent à }\widehat{DAI}}\\ &=\frac{DI}{DA}\\ &=\frac{DI}{4} \end{align*} \] Or I appartient à la droite (AM) donc \(\widehat{DAM}=\)\(\widehat{DAI}=53^{\circ}\).
\[ \begin{align*} &\tan \widehat{DAI}=\frac{DI}{4}\\ &DI=\tan \widehat{DAI}\times 4\\ &DI=\tan(53)\times 4\\ &DI\approx 5.3 \text{ cm} \end{align*} \] DI mesure 5,3 cm (arrondi au mm près).
Exercice 4 (Pondichéry avril 2015)
[AB] est un segment de milieu O tel que AB = 12 cm.Le point C appartient au cercle de centre O passant par A. De plus AC = 6 cm. L’angle \(\widehat{ABC}\) mesure 30°.
1) Figure en vraie grandeur :
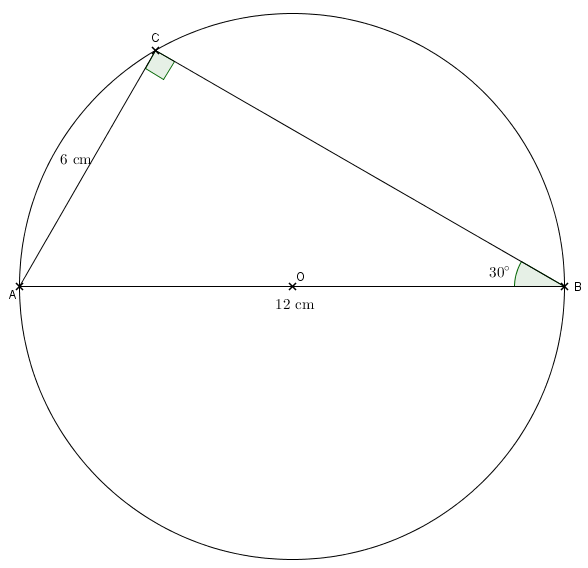
a) [AB] est un diamètre du
cercle de centre O et C un point de ce cercle donc le triangle ABC est
rectangle en C. L'affirmation est vraie.
b) Le triangle ABC est rectangle en C donc d'après le théorème de Pythagore :
\[ \begin{align*} &AC^{2}+BC^{2}=AB^{2}\\ &BC^{2}=AB^{2}-AC^{2}\\ &BC^{2}=12^{2}-6^{2}\\ &BC^{2}=144-36\\ &BC^{2}=108\\ &BC=\sqrt{108}\\ &BC=\sqrt{36}\times\sqrt{3}\\ &BC=6\sqrt{3}\text{ cm valeur exacte}\\ &BC \approx 10.39 \text{ cm valeur approchée} \end{align*} \] Le segment [BC] ne mesure pas exactement 10 cm, donc l'affirmation est fausse.
c) L'angle au centre \(\widehat{AOC}\) intercepte le même arc de cercle \(\overset{\frown}{AC}\) que l'angle inscrit \(\widehat{ABC}\) donc nous avons l'égalité suivante :
\[ \widehat{AOC}=2\times \widehat{ABC}=2\times 30=60^{\circ} \] L’angle \(\widehat{AOC}\) mesure 60°. L'affirmation est donc bien vraie.
d) Aire du triangle ABC :
\[ \begin{align*} A_{ABC}&=\frac{\text{Base}\times \text{ hauteur}}{2}\\ &=\frac{AC\times BC}{2}\\ &=\frac{6\times 6\sqrt{3}}{2}\\ &=18\sqrt{3} \end{align*} \] L’aire du triangle ABC est de \(18\sqrt{3}\) cm2. L'affirmation est donc vraie.
e) Le triangle BOC est isocèle en O donc \(\widehat{CBO}=\)\(\widehat{OCB}=30^{\circ}\)
La somme des angles du triangle BOC valant 180°, on en déduit la mesure de l'angle \(\widehat{BOC}\):
\[\widehat{BOC}=180-30-30=120^{\circ} \] \(\widehat{BOC}\) mesure 120°. La proposition est donc fausse.
b) Le triangle ABC est rectangle en C donc d'après le théorème de Pythagore :
\[ \begin{align*} &AC^{2}+BC^{2}=AB^{2}\\ &BC^{2}=AB^{2}-AC^{2}\\ &BC^{2}=12^{2}-6^{2}\\ &BC^{2}=144-36\\ &BC^{2}=108\\ &BC=\sqrt{108}\\ &BC=\sqrt{36}\times\sqrt{3}\\ &BC=6\sqrt{3}\text{ cm valeur exacte}\\ &BC \approx 10.39 \text{ cm valeur approchée} \end{align*} \] Le segment [BC] ne mesure pas exactement 10 cm, donc l'affirmation est fausse.
c) L'angle au centre \(\widehat{AOC}\) intercepte le même arc de cercle \(\overset{\frown}{AC}\) que l'angle inscrit \(\widehat{ABC}\) donc nous avons l'égalité suivante :
\[ \widehat{AOC}=2\times \widehat{ABC}=2\times 30=60^{\circ} \] L’angle \(\widehat{AOC}\) mesure 60°. L'affirmation est donc bien vraie.
d) Aire du triangle ABC :
\[ \begin{align*} A_{ABC}&=\frac{\text{Base}\times \text{ hauteur}}{2}\\ &=\frac{AC\times BC}{2}\\ &=\frac{6\times 6\sqrt{3}}{2}\\ &=18\sqrt{3} \end{align*} \] L’aire du triangle ABC est de \(18\sqrt{3}\) cm2. L'affirmation est donc vraie.
e) Le triangle BOC est isocèle en O donc \(\widehat{CBO}=\)\(\widehat{OCB}=30^{\circ}\)
La somme des angles du triangle BOC valant 180°, on en déduit la mesure de l'angle \(\widehat{BOC}\):
\[\widehat{BOC}=180-30-30=120^{\circ} \] \(\widehat{BOC}\) mesure 120°. La proposition est donc fausse.
Exercice 5 (Centres étrangers Maroc juin 2015)
Le triangle AOS est rectangle en A et nous souhaitons déterminer la longueur AS. A partir des informations de l'énoncé, nous pouvons utiliser la tangente de l'angle \(\widehat{SOA}\) :\[ \begin{align*} \tan{\widehat{SOA}}&=\frac{\text{côté opposé à }\widehat{SOA}}{\text{côté adjacent à }\widehat{SOA}}\\ &=\frac{AS}{AO} \end{align*} \] Et par conséquent :
\[ \begin{align*} &\tan(45)=\frac{AS}{15}\\ &\Leftrightarrow AS=15\times \tan(45)= 15\text{ mètres} \end{align*} \] AS mesure 15 mètres.
Le triangle AOP est rectangle en A et nous souhaitons déterminer la longueur AP. Nous allons utiliser la tangente de l'angle \(\widehat{AOP}\) :
\[ \begin{align*} \tan{\widehat{AOP}}&=\frac{\text{côté opposé à }\widehat{AOP}}{\text{côté adjacent à }\widehat{AOP}}\\ &=\frac{AP}{AO} \end{align*} \] Et par conséquent :
\[ \begin{align*} &\tan(25)=\frac{AP}{15}\\ &\Leftrightarrow AP=15\times \tan(25)\approx 6.99\text{ mètres} \end{align*} \] AP mesure environ 6.99 mètres.
La hauteur de l'arbre est égale à :
\[h=AS+AP\approx 15+6.99\approx 22\text{ m} \] (valeur arrondie au mètre près)
La hauteur de l'arbre est de 22 mètres environ.
Exercice 6 (Nouvelle-Calédonie décembre 2015)
Le triangle ABC est rectangle en B et on souhaite calculer la longueur AB connaissant BC et l'angle \(\widehat{CAB}\), nous allons donc utiliser la tangente de l'angle \(\widehat{CAB}\) :\[ \begin{align*} \tan{\widehat{CAB}}&=\frac{\text{côté opposé à }\widehat{CAB}}{\text{côté adjacent à }\widehat{CAB}}\\ &=\frac{BC}{AB} \end{align*} \] Et par conséquent :
\[ \begin{align*} &\tan(3)=\frac{30}{AB}\\ &\Leftrightarrow AB=\frac{30}{\tan(3)}\approx 572\text{ cm} \end{align*} \] AB mesure environ 572 cm.
Exercice 7 (France métropolitaine juin 2014)
1) Calcul du rapport :\[ \begin{align*} \frac{QK}{QP}&=\frac{QC-CK}{QP}\\ &=\frac{AP-CK}{QP}\\ &=\frac{0.65-0.58}{5}\\ &=0.014 \end{align*} \] Les feux de Pauline sont bien réglés avec une inclinaison égale à 0.014.
2) On remarque que le rapport \(\displaystyle{QK}{QP}\) n'est autre que la tangente de l'angle \(\widehat{QPK}\) :
\[ \begin{align*} \tan{\widehat{QPK}}&=\frac{\text{côté opposé à }\widehat{QPK}}{\text{côté adjacent à }\widehat{QPK}}\\ &=\frac{QK}{QP}\\ &=0.014 \end{align*} \] A l'aide de la calculatrice et de la touche tan-1, on trouve :
\(\widehat{QPK}\approx 0.8^{\circ}\)
L'angle \(\widehat{QPK}\) mesure approximativement 0.8°.
3) On peut soit utiliser le théorème de Thalès, soit les propriétés sur les angles. Nous exposons ici la deuxième méthode.
Les droites (AP) et (CQ) sont perpendiculaires à une même droite (AC) donc les droites (AP) et (CQ) sont parallèles. De plus, la droite (PS) est sécante à ces deux droites dons les angles alternes-internes \(\widehat{QPK}\) et \(\widehat{KSC}\) sont égaux :
\[\widehat{QPK}=\widehat{KSC}=\tan^{-1}(0.014)\approx 0.8^{\circ} \] Le triangle CKS étant rectangle en S, nous pouvons déterminer la longueur AS :
\[ \begin{align*} \tan\widehat{KSC}&=\frac{\text{côté opposé à }\widehat{KSC}}{\text{côté adjacent à }\widehat{KSC}}\\ &=\frac{KC}{CS}\\ &=\frac{0.58}{CS} \end{align*} \] Et par conséquent :
\[ \begin{align*} &\frac{0.58}{CS}=0.014\\ \Leftrightarrow & CS=\frac{0.58}{0.014}\approx 41.43\text{ mètres} \end{align*} \] On en déduit AS :
\[AS=AC+CS\approx 5+41.43 \approx 46.43 \text{ mètres} \] Compte-tenu de l'arrondi demandé, la distance d'éclairage des feux AS est de 46 mètres.
Exercice 8 (Centres étrangers juin 2014)
Réalisons un petit schéma :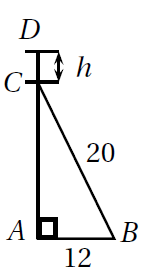
\[ \begin{align*} &AB^{2}+AC^{2}=BC^{2}\\ &AC^{2}=BC^{2}-AB^{2}\\ &AC^{2}=20^{2}-12^{2}\\ &AC^{2}=400-144\\ &AC^{2}=256\\ &AC=\sqrt{256}=16 \text{ pieds} \end{align*} \] AC mesure 16 pieds. On en déduit la hauteur \(h\) :
\[h=AD-AC=20-16=4 \] L'extrémité de la lance descend de 4 pieds le long du mur.