POLYNESIE JUIN 2016
|
Exercice 1 (6 points)
 Le Solitaire
est un jeu de hasard de la Française des Jeux.
Le Solitaire
est un jeu de hasard de la Française des Jeux.Le joueur achète un ticket au prix de 2€, gratte la case argentée et découvre le «montant du gain ».
Un ticket est gagnant si le «montant du gain » est supérieur ou égal à 2€.
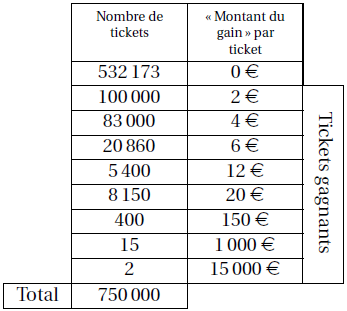
Les tickets de Solitaire sont fabriqués par lots de 750 000 tickets.
Le tableau ci-contre donne la composition d’un lot.
1) Si on prélève un ticket au hasard dans un lot :
a) quelle est la
probabilité d’obtenir un ticket gagnant dont le « montant du gain » est
4€ ?
b) quelle est la probabilité d’obtenir un ticket gagnant ?
c) expliquer pourquoi on a moins de 2% de chance d’obtenir un ticket dont le « montant du gain » est supérieur ou égal à 10 €.
2) Tom dit : « Si j’avais assez d’argent, je pourrais acheter un lot
complet de tickets Solitaire. Je deviendrais encore plus riche. »
Expliquer si Tom a raison.b) quelle est la probabilité d’obtenir un ticket gagnant ?
c) expliquer pourquoi on a moins de 2% de chance d’obtenir un ticket dont le « montant du gain » est supérieur ou égal à 10 €.
Exercice 2 (6 points)
Voici un programme de calcul :| •
Choisir un nombre entier positif • Ajouter 1 • Calculer le carré du résultat obtenu • Enlever le carré du nombre de départ. |
1) On applique ce programme de calcul au nombre 3. Montrer qu’on obtient 7.
2) Voici deux affirmations :
Affirmation n°1 : « Le chiffre des unités du résultat obtenu est 7 ».
Affirmation n°2 : « Chaque résultat peut s’obtenir en ajoutant le nombre entier de départ et le nombre entier qui le suit ».
a) Vérifier que ces deux
affirmations sont vraies pour les nombres 8 et 13.
b) Pour chacune de ces deux affirmations, expliquer si elle est vraie ou fausse quel que soit le nombre choisi au départ.
b) Pour chacune de ces deux affirmations, expliquer si elle est vraie ou fausse quel que soit le nombre choisi au départ.
Exercice 3 (6 points)
 Dans la
figure ci-contre :
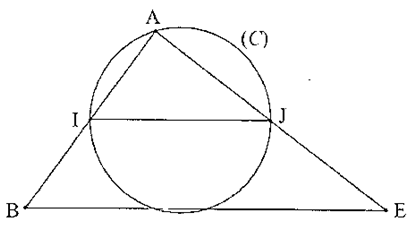
Dans la
figure ci-contre :• ABE est un triangle ;
• AB = 6 cm, AE = 8 cm et BE = 10 cm ;
• I et J sont les milieux respectifs des côtés [AB] et [AE] ;
• le cercle (C) passe par les points I, J et A.
La figure n’est pas à l’échelle.• AB = 6 cm, AE = 8 cm et BE = 10 cm ;
• I et J sont les milieux respectifs des côtés [AB] et [AE] ;
• le cercle (C) passe par les points I, J et A.
1) Peut-on affirmer que les droites (IJ) et (BE) sont parallèles ?
2) Montrer que le triangle ABE est rectangle.
3) Quelle est la mesure de l’angle \(\widehat{AEB}\) ? On donnera une valeur approchée au degré près.
4)
a) Justifier que le centre
du cercle (C) est le milieu du segment
[IJ].
b) Quelle est la mesure du rayon du cercle (C) ?
b) Quelle est la mesure du rayon du cercle (C) ?
Exercice 4 (7 points)
Une association cycliste organise une journée de randonnée à vélo.Les participants ont le choix entre trois circuits de longueurs différentes : 42 km, 35 km et 27 km.
À l’arrivée, les organisateurs relèvent les temps de parcours des participants et calculent leurs vitesses moyennes. Ils regroupent les informations dans un tableau dont voici un extrait :
| Nom du sportif | Alix | David | Gwenn | Yassin | Zoé |
| Distance parcourue (en km) | 35 | 42 | 27 | 35 | 42 |
| Durée de la randonnée | 2 h | 3 h | 1 h 30 min | 1 h 45 min | 1 h 36 min |
| Vitesse moyenne (en km/h) | 17,5 |
1) Quelle distance David a-t-il parcourue ?
2) Calculer les vitesses moyennes de David et de Gwenn.
3) Afin d’automatiser les calculs, l’un des organisateurs décide d’utiliser la feuille de tableur ci-dessous :
| A | B | C | D | E | F | |
| 1 | Nom du sportif | Alix | David | Gwenn | Yassin | Zoé |
| 2 | Distance parcourue (en km) | 35 | 42 | 27 | 35 | 42 |
| 3 | Durée de la randonnée | 2 | 3 | 1.5 | ||
| 4 | Vitesse moyenne (en km/h) | 17,5 |
a) Quel nombre doit-il saisir dans la cellule E3 pour renseigner le temps de Yassin ?
b) Expliquer pourquoi il doit saisir 1,6 dans la cellule F3 pour renseigner le temps de Zoé.
c) Quelle formule de tableur peut-il saisir dans la cellule B4 avant de l’étirer sur la ligne 4 ?
Sa montre GPS indique qu’il a fait le circuit de 35 km à la vitesse moyenne de 25 km/h.
Combien de temps a-t-il mis pour faire sa randonnée ? On exprimera la durée de la randonnée en heures et minutes.
Exercice 5 (4 points)
On découpe la pyramide FIJK dans le cube ABCDEFGH comme le montre le dessin ci-dessous.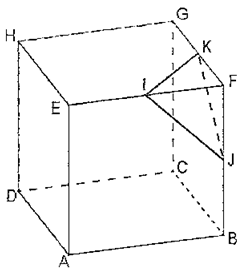
Les points I, J, et K sont les milieux respectifs des arêtes [FE], [FB] et [FG].
1) Tracer le triangle IFK en vraie grandeur.
2) Un des quatre schémas ci-dessous correspond au patron de la pyramide FIJK.
Indiquer son numéro sur la copie. Aucune justification n’est attendue.
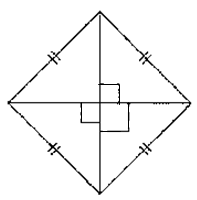 Schéma 1 |
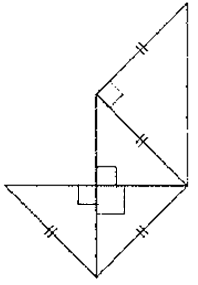 Schéma 2 |
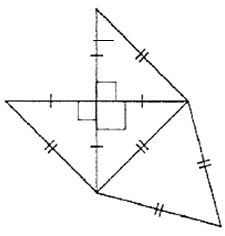 Schéma 3 |
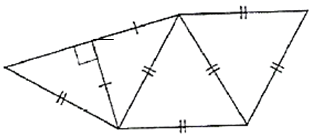 Schéma 4 |
3) Calculer le volume de la pyramide FIJK.
Rappel :
\[V_{\text{pyramide }}= \frac{\text{Aire d'une base}\times \text{hauteur}}{3}\]
Exercice 6 (4 points)
M. Durand doit changer de voiture. Il choisit un modèle PRIMA qui existe en deux versions : ESSENCE ou DIESEL. Il dispose des informations suivantes :Modèle
PRIMA |
Version
ESSENCE Consommation moyenne : 6,2 L pour 100 km Type de moteur : essence Carburant : SP 95 Prix d'achat : 21 550 € |
VERSION
DIESEL Consommation moyenne : 5,2 L pour 100 km Type de moteur : diesel Carburant : gazole Prix d'achat : 23 950€ |
|
Estimation du prix
des carburants par
• Prix d’un litre de SP 95 : 1,415€M. Durand en 2015 • Prix d’un litre de gazole : 1,224€ |
Durant les dernières années, M. Durand a parcouru en moyenne 22 300 km par an.
Pour choisir entre les deux modèles, il décide de réaliser le tableau comparatif ci-dessous, établi pour 22 300 km parcourus en un an.
| Version ESSENCE | Version DIESEL | |
| Consommation de carburant (en L) | 1 383 | |
| Budget de carburant (en €) | 1 957 |
1) Recopier et compléter le tableau sur la copie en écrivant les calculs effectués.
2) M. Durand choisit finalement la version DIESEL.
En considérant qu’il parcourt 22 300 km tous les ans et que le prix du carburant ne varie pas, dans combien d’années l’économie réalisée sur le carburant compensera-t-elle la différence de prix d’achat entre les deux versions ?
Exercice 7 (3 points)
Les continents occupent 5/17 de la superficie totale de la Terre.1) L’Océan Pacifique recouvre la moitié de la superficie restante. Quelle fraction de la superficie totale de la Terre occupe-t-il ?
2) Sachant que la superficie de l’océan Pacifique est de 180 000 000 km2, déterminer la superficie de la Terre.