FRANCE JUIN 2016
|
Exercice 1 (4 points)
| Usine A | Usine B | |
| Bons | 473 | 462 |
| Défectueux | 27 | 38 |
1) Parmi les 500 composants prélevés dans l'usine A, 27 sont défectueux.
La probabilité qu'un composant tiré au hasard parmi ceux provenant de l’usine A soit défectueux est égale à :
\[\frac{27}{500}=0.054\]
2) Nombre total de composants défectueux : 27 + 38 = 65
Il y a 65 composants défectueux. Parmi ceux-ci, 27 proviennent de l'usine A donc la probabilité qu'un composant tiré au hasard parmi ceux qui sont défectueux provienne de l'usine A est égale à :
\[\frac{27}{65}\approx 0.415\]
3) Dans l'usine A, le taux de composants défectueux est de 0.054, soit 5.4% ce qui est inférieur à 7%. Le contrôle est satisfaisant dans l'usine A.
Dans l'usine B, le taux de composants défectueux est égal à :
\[\frac{38}{500}=0.076=7.6\%\] Le taux est de 7.6% dans l'usine B ce qui est supérieur à 7% ; par conséquent le contrôle n'est pas satisfaisant dans l'usine B.
Exercice 2 (4.5 points)
On considère les deux programmes de calcul ci-dessous.| Programme A | Programme B |
| 1.
Choisir un nombre. 2. Multiplier par -2. 3. Ajouter 13. |
1.
Choisir un nombre. 2. Soustraire 7. 3. Multiplier par 3. |
1) Avec le programme A
Choisir un nombre : \(2\)
Multiplier par -2 : \(2\times(-2)=-4\)
Ajouter 13 : \(-4+13=9\)
2) Avec le programme B, en appelant \(x\) le nombre de départ.
Choisir un nombre : \(x\)
Soustraire 7 : \(x-7\)
Multiplier par 3 : \(3(x-7)=3x-21\)
Lorsque \(x\) est le nombre de départ avec le programme B, le nombre d'arrivée est \(3x-21\). On souhaite que le nombre d'arrivée soit égal à 9. On doit donc résoudre l'équation suivante :
\[\begin{align*} &3x-21=9\\ &3x=9+21\\ &3x=30\\ &x=\frac{30}{3}\\ &x=10 \end{align*}\] Pour obtenir 9 comme nombre d'arrivée avec le programme B, il faut choisir 10 comme nombre de départ.
3) Avec le programme A, en appelant \(x\) le nombre de départ.
Choisir un nombre : \(x\)
Multiplier par -2 : \(x\times(-2)=-2x\)
Ajouter 13 : \(-2x+13\)
Lorsque \(x\) est le nombre de départ avec le programme A, le nombre d'arrivée est \(-2x-13\).
Pour avoir le même nombre d'arrivée avec le programme A et le programme B, on doit résoudre l'équation suivante :
\[\begin{align*} &-2x+13=3x-21\\ &13+21=3x+2x\\ &5x=34\\ &x=\frac{34}{5}\\ &x=6.8 \end{align*}\] Il faut choisir 6.8 comme nombre de départ pour obtenir le même résultat avec les deux programmes.
Exercice 3 (5 points)
Figure 1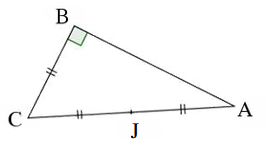 BC = 6 cm |
Figure 2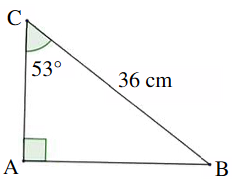 |
Figure 3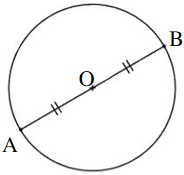 [AB] est un diamètre du cercle de centre O. La longueur du cercle est 154 cm. |
|
1) Figure 1
Le triangle ABC est rectangle en B avec BC = 6 cm et AC = 12 cm (d'après les codages) donc d'après le théorème de Pythagore :
\[\begin{align*} &AB^{2}+BC^{2}=AC^{2}\\ &AB^{2}=AC^{2}-BC^{2}\\ &AB^{2}=12^{2}-6^{2}\\ &AB^{2}=144-36\\ &AB^{2}=108\\ &AB=\sqrt{108}\\ &AB=\sqrt{36\times 3}\\ &AB=\sqrt{36}\times \sqrt{3}\\ &AB=6\sqrt{3}\text{ cm (valeur exacte)}\\ &AB\approx 10.4\text{ cm (valeur arrondie au mm)} \end{align*} \] AB mesure approximativement 10.4 cm (valeur arrondie au mm).
2) Figure 2
Le triangle ABC est rectangle en A, on peut utiliser les formules trigonométriques pour déterminer la longueur AB :
\[ \begin{align*} &\sin{\widehat{ACB}}=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{hypoténuse}}=\frac{AB}{BC}\\ &\sin{(53)}=\frac{AB}{36}\\ &AB=\sin{53}\times 36\\ &AB\approx 28.8\text{ cm (valeur arrondie au mm)} \end{align*}\] AB mesure approximativement 28.8 cm (valeur arrondie au mm).
3) Figure 3
Le périmètre du cercle étant de 154 cm :
\[\begin{align*} &P=2\pi\times r\\ &P=2\pi\times OB\\ &P=\pi \times AB\\ &AB=\frac{P}{\pi}\\ &AB=\frac{154}{\pi}\\ &AB\approx 49\text{ cm (valeur arrondie au mm)} \end{align*}\] AB mesure approximativement 49 cm (valeur arrondie au mm).
Exercice 4 (5 points)
1) Prix après réduction :\[54\times\left(1-\frac{30}{100}\right)=54\times 0.7=37.8\] Cet article coûtera 37€80 après réduction.
2)

a) En B2, il a dû saisir
la formule suivante :
=B1*0.3
b) En B3, il a dû saisir la formule suivante :
=B1-B2
=B1*0.3
b) En B3, il a dû saisir la formule suivante :
=B1-B2
3) Soit \(x\) le prix initial. On applique une réduction de 30% pour obtenir le nouveau prix :
\[x\times \left(1-\frac{30}{100}\right)=0.7x\] Le nouveau prix vaut 42€. On en déduit le prix initial :
\[\begin{align*} &42=0.7x\\ &x=\frac{42}{0.7}\\ &x=60 \end{align*}\] Le prix initial était de 60€.
Exercice 5 (5,5 points)
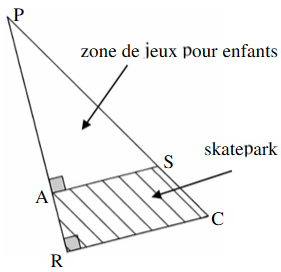
1) Surface de la zone PAS :
\[A_{PAS}=\frac{PA \times AS}{2}=\frac{30 \times 18}{2}=270\text{ m}^{2}\] La surface de la zone de jeux est de 270 m2.
Sachant qu'un sac permet de couvrir 140 m2, il faudra deux sacs pour couvrir 270 m2, soit un budget de :
\[13.90\times 2=27€80\] Il faudra 27€80 de budget pour couvrir la zone de jeux pour enfants de gazon.
2) Il faut d'abord calculer la longueur RC.
Les droites (AS) et (RC) sont perpendiculaires à la même droite (PR), donc (AS) est parallèle à (RC). On peut donc utiliser le théorème de Thalès pour calculer la longueur RC :
\[\begin{align*} &\frac{PA}{PR}=\frac{PS}{PC}=\frac{AS}{RC}\\ &\frac{PA}{PA+AR}=\frac{PS}{PC}=\frac{AS}{RC}\\ &\frac{30}{30+10}=\frac{PS}{PC}=\frac{18}{RC}\\ \end{align*}\] On cherche à calculer la longueur RC :
\[\begin{align*} &0.75=\frac{18}{RC}\\ &RC=\frac{18}{0.75}\\ &RC=24\text{ m} \end{align*}\] RC mesure 24 mètres.
Deux possibilités pour calculer l'aire du skatepark :
a) ASCR est un trapèze
donc :
\[ \begin{align*} A_{ASCR}&=\frac{(b+B) \times h}{2}\\ &=\frac{(AS+RC)\times AR}{2}\\ &=\frac{(18+24)\times 10}{2}\\ &=210\text{ m}^{2} \end{align*} \] La superficie du skatepark est de 210 m2.
b) Aire du triangle PRC :
\[ \begin{align*} A_{PRC}&=\frac{PR \times RC}{2}\\ &=\frac{40\times 24}{2}\\ &=480\text{ m}^{2} \end{align*} \] L'aire du triangle PRC est de 480 m2. On en déduit l'aire du trapèze ASRC :
\[ \begin{align*} A_{ASCR}&=A_{PRC}-A_{PAS}\\ &=480-270\\ &=210\text{ m}^{2} \end{align*} \] La superficie du skatepark est de 210 m2.
\[ \begin{align*} A_{ASCR}&=\frac{(b+B) \times h}{2}\\ &=\frac{(AS+RC)\times AR}{2}\\ &=\frac{(18+24)\times 10}{2}\\ &=210\text{ m}^{2} \end{align*} \] La superficie du skatepark est de 210 m2.
b) Aire du triangle PRC :
\[ \begin{align*} A_{PRC}&=\frac{PR \times RC}{2}\\ &=\frac{40\times 24}{2}\\ &=480\text{ m}^{2} \end{align*} \] L'aire du triangle PRC est de 480 m2. On en déduit l'aire du trapèze ASRC :
\[ \begin{align*} A_{ASCR}&=A_{PRC}-A_{PAS}\\ &=480-270\\ &=210\text{ m}^{2} \end{align*} \] La superficie du skatepark est de 210 m2.
Exercice 6 (7 points)
Partie 11) Si le morceau n°1 mesure 8 cm, on obtient un carré de 2 cm de côté. Il reste alors 12 cm, et on obtient un triangle équilatéral dont la longueur de chaque côté est de 4 cm :
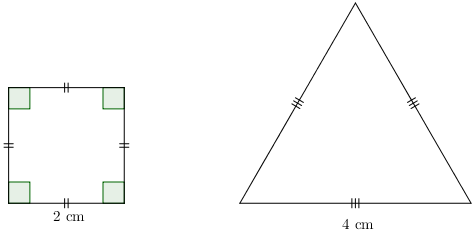
2) Calcul de l'aire du carré :
\[A_{\text{carré}}=2^{2}=4\text{ cm}^{2}\] L'aire du carré est de 4 cm2.
3) La hauteur du triangle mesure approximativement 3.4 cm. On en déduit l'aire du triangle :
\[A_{\text{triangle}}\approx\frac{4\times 3.4}{2}=6.8\text{ cm}^{2}\] L'aire du triangle est approximativement de 6.8 cm2.
Partie 2
1) Si on appelle \(x\) la longueur du morceau n°1, alors la longueur de chaque côté du carré est égale à :
\[\frac{x}{4}\] L'aire du carré est alors égale à :
\[\left(\frac{x}{4}\right)^{2}=\frac{x^{2}}{16}\]
2)
Graphique représentant les aires
des polygones en fonction de la longueur
du «morceau n° 1 »
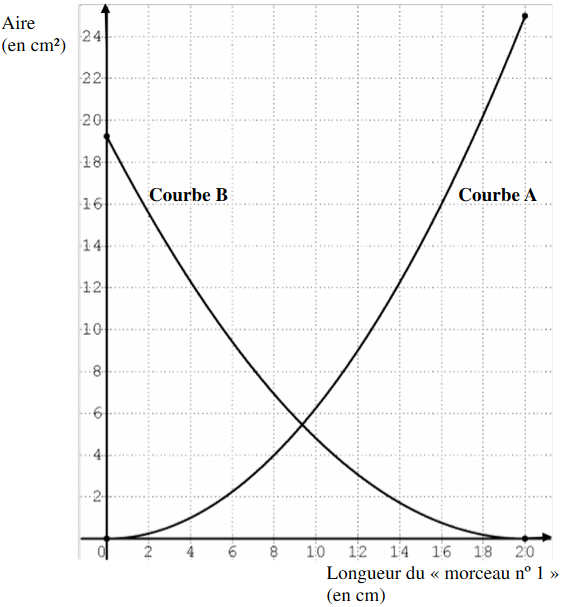
du «morceau n° 1 »

a) Il faut
regarder la courbe B. Pour obtenir un triangle ayant une aire de 14 cm2,
il faut que le morceau n°1 mesure environ 3 cm.
b) On regarde le point d'intersection des deux courbes. Il faut que le morceau n°1 mesure environ 9.5 cm.
b) On regarde le point d'intersection des deux courbes. Il faut que le morceau n°1 mesure environ 9.5 cm.
Exercice 7 (5 points)
Caractéristiques du vase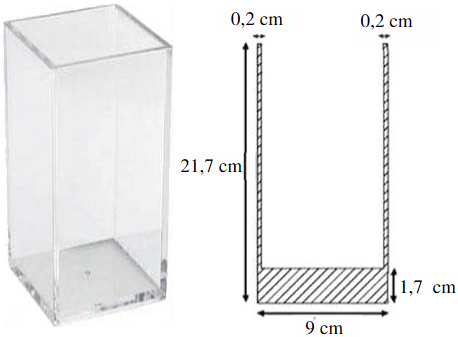 Matière : verre Forme : pavé droit Dimensions extérieures : 9 cm × 9 cm × 21,7 cm Épaisseur des bords : 0,2 cm Épaisseur du fond : 1,7 cm |
Caractéristiques des billes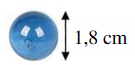 Matière : verre Forme : boule Dimension : 1,8 cm de diamètre |
Pour calculer le volume remplissable du vase, sa hauteur est égale à :
\[h=21.7-1.7=20\text{ cm}\] La base du vase est un carré de 9 cm. Mais il faut enlever les bordures. Chaque côté du carré mesure :
\[c=9-0.2-0.2=8.6\text{ cm}\] On en déduit le volume du vase :
\[V_{\text{vase}}=c\times c\times h = 8.6^{2}\times 20=1479.2 \text{ cm}^{3}\] Le volume remplissable du vase est de 1479.2 cm3.
Le diamètre d'une bille est de 1.8 cm, donc le rayon est de 0.9 cm.
Calcul du volume d'une bille :
\[\begin{align*} V_{\text{bille}}&=\frac{4}{3}\times\pi\times r^{3}\\ &=\frac{4}{3}\times \pi \times 0.9^{3}\\ &=0.972\pi \text{ cm}^{3} \end{align*}\] Le volume d'une bille est de \(0.972 \pi\) cm3.
Volume des 150 billes :
\[150\times 0.972\pi=145.8\pi \text{ cm}^{3}\] Volume restant pour l'eau :
\[1479.2-145.8\pi\approx 1021.16 \text{ cm}^{3}\] Le volume restant pour l'eau est de 1021.16 cm3. Transformons ce volume en litre(s) :
\[1021.16 \text{ cm}^{3}=1.02116\text{ dm}^{3}=1.02116\text{ litre}\] Comme 1.02116 est supérieur à 1, Antoine pourra ajouter un litre d'eau colorée sans risquer le débordement.