CENTRES ETRANGERS 1 JUIN 2015
|
Les figures ou croquis ne sont pas en vraie grandeur !
Pour chaque question, laisser toutes traces de la recherche : même non aboutie, elle sera valorisée.
Exercice 1 (5,5 points)
| 1 |
2 |
3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
1)
a) Il y a neuf cases donc
la probabilité que la case 1 s'allume est égale
à \( \displaystyle \frac{1}{9}\).
b) Les chiffres impairs sont 1, 3, 5, 7 et 9. Ils sont donc au nombre de 5. La probabilité qu'un chiffre impair s'allume est égale à \( \displaystyle \frac{5}{9}\).
c) "Obtenir un multiple de 3" est un évènement dont la probabilité est égale à 1/3. On peut également citer :
"Obtenir un nombre strictement supérieur à 6"
"Obtenir un nombre supérieur ou égal à 7"
"Obtenir un nombre strictement inférieur à 4"
"Obtenir un nombre inférieur ou égal à 4"
etc
2) Sachant que 1 et 7 sont allumées, il n'y a que 4 comme possibilité
pour obtenir trois cases allumées alignées. Sachant qu'il ne reste que
7 cases éteintes possibles à allumer, la probabilité d'obtenir 3 cases
allumées sachant que 1 et 7 sont déjà allumées est égale à \( \displaystyle \frac{1}{7}\).
b) Les chiffres impairs sont 1, 3, 5, 7 et 9. Ils sont donc au nombre de 5. La probabilité qu'un chiffre impair s'allume est égale à \( \displaystyle \frac{5}{9}\).
c) "Obtenir un multiple de 3" est un évènement dont la probabilité est égale à 1/3. On peut également citer :
"Obtenir un nombre strictement supérieur à 6"
"Obtenir un nombre supérieur ou égal à 7"
"Obtenir un nombre strictement inférieur à 4"
"Obtenir un nombre inférieur ou égal à 4"
etc
Exercice 2 (4 points)
1) Exprimons cette vitesse en m/s :\[ \begin{align*} 1357.6\text{ km/h}&=1357600\text{ m/h}\\ &=\frac{1357600}{3600}\text{ m/s}\\ & \approx 377.11\text{ m/s} \end{align*} \] Sa vitesse maximale ayant été de 377.11 m/s, il a donc bien franchi le mur du son (340 m/s).
2)
| Altitude du saut | 38 969,3 m |
| Distance parcourue en chute libre | 36 529 m |
| Durée totale du saut | 9 min 3 s |
| Durée de la chute libre | 4 min 19 s |
Distance parcourue en parachute :
\[38969.3-36529=2440.3\text{ m}\] Il a parcouru 2440.3 mètres en parachute.
Durée du saut en parachute :
9 min 3 s - 4 min 19 s = 4 min 44 s
Transformons 4 min 44 s en secondes :
\[4\text{ min } 44\text{ s}=4\times 60 +44\text{ s}=284\text{ s}\] Il a mis 284 secondes pour toucher le sol. Sa vitesse en parachute est donc égale à :
\[\frac{2440.3}{284}\approx 8.6\text{ m/s} \]
Soit une vitesse approximative de 9 m/s (valeur arrondie à l'unité).
Exercice 3 (6 points)
1) Figure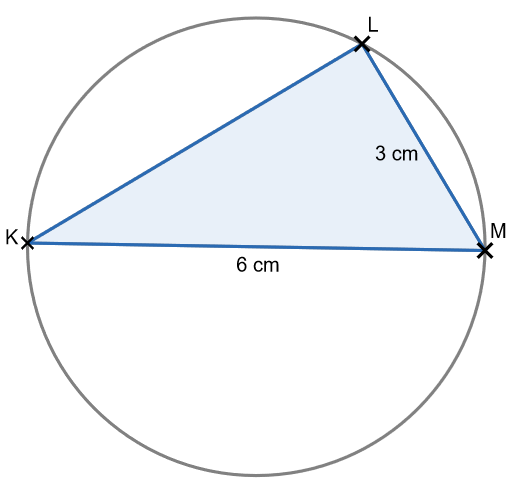
2) [KM] est un diamètre du cercle et L un point de ce cercle donc le triangle KLM est rectangle en L.
Calculons la longueur KL pour déterminer ensuite l'aire du triangle KLM.
Le triangle KLM est rectangle en L donc d'après le théorème de Pythagore : \[ \begin{align*} &KL^{2}+LM^{2}=KM^{2}\\ &KL^{2}=KM^{2}-LM^{2}\\ &KL^{2}=6^{2}-3^{2}\\ &KL^{2}=36-9\\ &KL^{2}=27\\ &KL=\sqrt{27}\\ &KL=\sqrt{9\times 3}\\ &KL=\sqrt{9}\times \sqrt{3}\\ &KL=3\sqrt{3}\text{ cm} \end{align*} \] KL mesure \(3\sqrt{3}\) cm.
Aire du triangle KLM : \[ \begin{align*} A_{KLM}&=\frac{\text{Base }\times\text{ Hauteur}}{2}\\ &=\frac{KL \times LM}{2}\\ &=\frac{3\sqrt{3}\times 3}{2}\\ &=\frac{9}{2}\sqrt{3}\text{ cm}^{3}\text{ (valeur exacte)}\\ &\approx 8\text{ cm}^{3}\text{ (valeur arrondie)}\\ \end{align*} \] L'aire du triangle KLM est d'environ 8 cm3.
Exercice 4 (6 points)
1)
a) Dans la cellule B2, on doit saisir la formule :
=9*B1-8
b) Dans la cellule B3, on doit saisir la formule :
=-3*B1+31
2) =9*B1-8
b) Dans la cellule B3, on doit saisir la formule :
=-3*B1+31

3) Appelons \(x\) le nombre de départ. On doit résoudre l'équation suivante :
\[ \begin{align*} &9x-8=-3x+31\\ &9x+3x=31+8\\ &12x=39\\ &x=\frac{39}{12}\\ &x=3.25 \end{align*} \] Le nombre de départ doit être 3.25, qui est bien compris entre 3 et 4.
Exercice 5 (8 points)
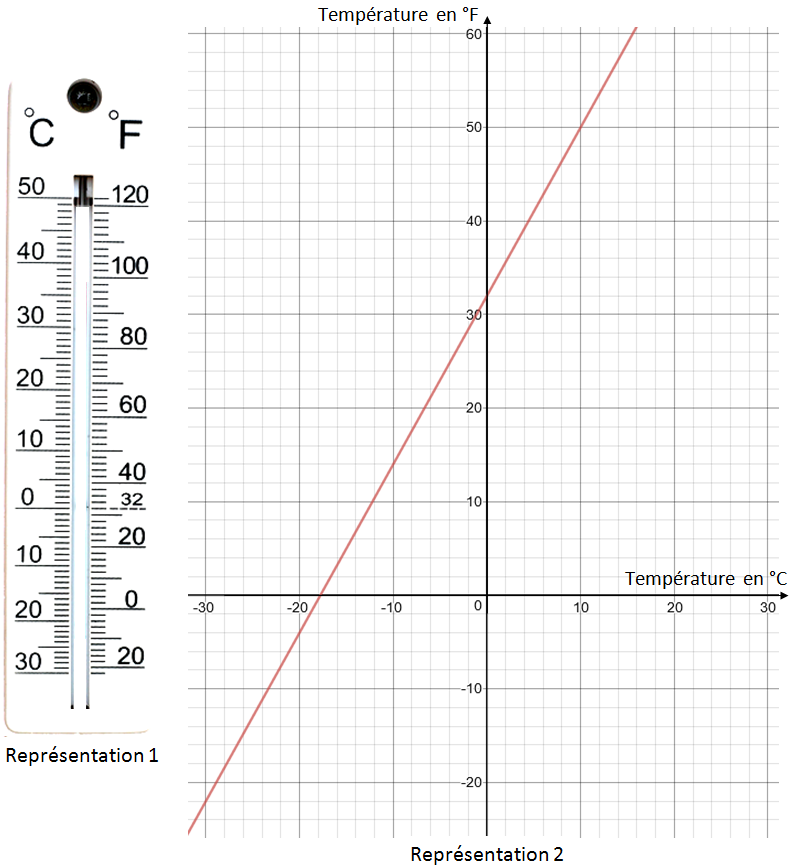
2) Graphiquement, 0°C correspond à 32°F. Avec la proposition 3, nous avons : \[ \begin{align*} f(0)&=2\times 0+30\\ &=30\\ &\neq 32 \end{align*} \] donc la proposition 3 est fausse.
Graphiquement, 10°C correspond à 50°F. Avec la proposition 1, nous avons : \[ \begin{align*} f(10)&=10+32\\ &=42\\ &\neq 50 \end{align*} \] donc la proposition 1 est fausse.
Par élimination, on en déduit que la proposition 2 est correcte.
3)
\[ \begin{align*} f(10)&=1.8\times 10+32\\ &=18+32\\ &= 50 \end{align*} \] Et \[ \begin{align*} f(-40)&=1.8\times (-40)+32\\ &=-72+32\\ &=-40 \end{align*} \]
4) A la question 3, nous avons montré que \(f(-40)=-40\). Cela signifie qu'il existe bien une valeur pour laquelle la température exprimée en degré Celsius est égale à la température exprimée en degré Fahrenheit : -40°C correspond à la même température que -40°F.
Exercice 6 (6,5 points)
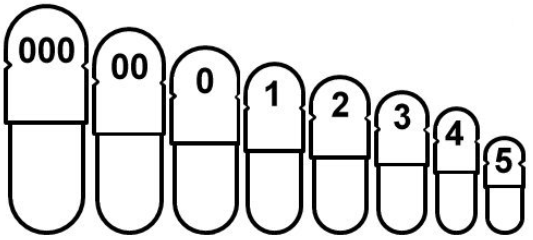
| Calibre de la gélule | 000 | 00 | 0 | 1 | 2 | 3 | 4 | 5 |
| Longueur L de la gélule (en mm) | 26.1 | 23.3 | 21.7 | 19.4 | 18.0 | 15.9 | 14.3 | 11.1 |
Source : « Technical Reference
File 1st edition CAPSUGEL - Gélules Coni-Snap
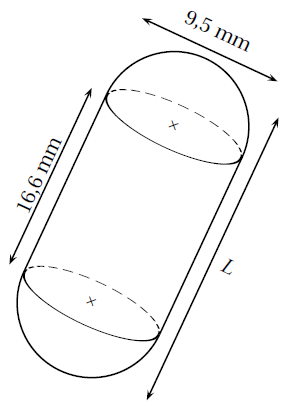
Cette représentation n’est pas en vraie grandeur.
1) La longueur L de cette gélule est de 16.6 mm plus le diamètre d'une sphère (puisque nous avons deux demi-sphères) : \(L=16.6+9.5=26.1\text{ mm}\) Il s'agit d'une gélule de calibre 000.
2) Le volume de cette gélule est le volume d'un cylindre plus le volume d'une sphère.
Calcul du volume du cylindre : \[ \begin{align*} V_{\text{cylindre}}&=\pi\times R^{2}\times h \\ &=\pi \times \left(\frac{9.5}{2}\right)^{2}\times 16.6 \\ &=374.5375\pi\\ &\approx 1176.643\text{ mm}^{3} \end{align*} \] Calcul du volume de la sphère : \[ \begin{align*} V_{\text{sphère}}&=\frac{4}{3}\times \pi\times R^{3} \\ &=\frac{4}{3}\times \pi\times \left(\frac{9.5}{2}\right)^{3}\\ &\approx 448.920\text{ mm}^{3} \end{align*} \] Le volume de la gélule est donc égal à : \[ \begin{align*} V_{\text{gélule}}&=V_{\text{cylindre}}+V_{\text{sphère}} \\ &\approx 1176.643+448.920 \\ &\approx 1626\text{ mm}^{3} \end{align*} \] Le volume de la gélule est approximativement de 1626 mm3.
3) Chaque boîte contient 18 gélules.
Volume total des gélules : \[ V_{\text{antibiotique}}\approx 18\times 1626\approx 29268 \text{ mm}^{3} \] Etant donné que la masse volumique est le rapport entre la masse et le volume, la masse d'antibiotiques absorbée par Robert pendant son traitement est égale à : \[ m_{\text{antibiotique}}\approx 6.15\times 10^{-4}\times 29268\approx 18\text{ g} \] Robert a absorbé environ 18 grammes d'antibiotiques pendant son traitement.