POLYNESIE JUIN 2016
|
Exercice 1 (6 points)
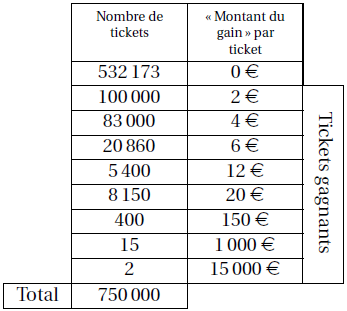
a) 83 000 tickets
permettent de gagner 4€ sachant qu'il y a 750 000
tickets ; la probabilité de gagner 4€ est donc égale à :
\[\frac{83000}{750000}\approx 0.111\] La probabilité de gagner 4€ est approximativement de 0.111.
b) Nombre de tickets gagnants (2€ ou plus) :
\[100000+83000+20860+...+2=217827\] Ou plus rapidement :
\[750000-532173=217827\] Il y a 217 827 tickets gagnants.
La probabilité d'obtenir un ticket gagnant est égale à :
\[\frac{217827}{750000}\approx 0.29\] La probabilité d'obtenir un ticket gagnant est approximativement de 0.29.
c) Nombre de tickets dont le gain est supérieur ou égal à 10€ :
\[5400+8150+400+15+2=13967\] La probabilité d'obtenir un gain supérieur à 10€ est égale à :
\[\frac{13967}{750000}\approx 0.0186\approx 1.86\%\] On a environ 1.86% de chance (soit moins de 2%) d'obtenir un ticket dont le montant du gain est supérieur ou égal à 10€.
\[\frac{83000}{750000}\approx 0.111\] La probabilité de gagner 4€ est approximativement de 0.111.
b) Nombre de tickets gagnants (2€ ou plus) :
\[100000+83000+20860+...+2=217827\] Ou plus rapidement :
\[750000-532173=217827\] Il y a 217 827 tickets gagnants.
La probabilité d'obtenir un ticket gagnant est égale à :
\[\frac{217827}{750000}\approx 0.29\] La probabilité d'obtenir un ticket gagnant est approximativement de 0.29.
c) Nombre de tickets dont le gain est supérieur ou égal à 10€ :
\[5400+8150+400+15+2=13967\] La probabilité d'obtenir un gain supérieur à 10€ est égale à :
\[\frac{13967}{750000}\approx 0.0186\approx 1.86\%\] On a environ 1.86% de chance (soit moins de 2%) d'obtenir un ticket dont le montant du gain est supérieur ou égal à 10€.
2) Si Tom achète un lot de 750000 tickets à 2€, cela va lui coûter :
\[750000\times 2=1500000€\] La somme qu'il va gagner est égale à :
\[ \begin{align*} &100000\times 2+83000\times 4+...+2\times 15000\\ &=989960€ \end{align*}\] Cela lui coûte plus cher que cela ne lui rapporte, par conséquent Tom a tort.
Exercice 2 (6 points)
| •
Choisir un nombre entier positif • Ajouter 1 • Calculer le carré du résultat obtenu • Enlever le carré du nombre de départ. |
1) En prenant 3 comme nombre de départ :
• Choisir un nombre entier positif : 3
• Ajouter 1 : \(3+1=4\)
• Calculer le carré du résultat obtenu \(4^{2}=16\)
• Enlever le carré du nombre de départ. \(16-3^{2}=16-9=7\)
2)
a) Lorsque le nombre de
départ est 8 :
• Choisir un nombre entier positif : 8
• Ajouter 1 : \(8+1=9\)
• Calculer le carré du résultat obtenu \(9^{2}=81\)
• Enlever le carré du nombre de départ. \(81-8^{2}=81-64=17\)
Dans ce cas, l'affirmation 1 est vraie (17 se termine par 7) ainsi que l'affirmation 2 (17 est bien égal au nombre de départ 8 auquel on ajoute le nombre entier qui le suit 9).
Lorsque le nombre de départ est 13 :
• Choisir un nombre entier positif : 13
• Ajouter 1 : \(13+1=14\)
• Calculer le carré du résultat obtenu \(14^{2}=196\)
• Enlever le carré du nombre de départ. \(196-13^{2}=196-169=27\)
Dans ce cas, l'affirmation 1 est vraie (27 se termine par 7) ainsi que l'affirmation 2 (27 est bien égal au nombre de départ 13 auquel on ajoute le nombre entier qui le suit 14).
b) Si on appelle \(x\) le nombre de départ :
• Choisir un nombre entier positif : \(x\)
• Ajouter 1 : \(x+1\)
• Calculer le carré du résultat obtenu \((x+1)^{2}\)
• Enlever le carré du nombre de départ. \((x+1)^{2}-x^{2}=(x+1+x)(x+1-x)=2x+1\)
Lorsque le nombre de départ est \(x\), le résultat obtenu est \(2x+1\).
Concernant l'affirmation 1, elle est fausse : prenons par exemple 4 comme nombre de départ, on obtient :
\(2x+1=2\times 4+1=9\) qui ne se termine pas par 7.
Concernant l'affirmation 2, lorsqu'on additionne deux nombres consécutifs, le résutat obtenu est :
\(x+(x+1)=2x+1\)
ce qui est le résultat obtenu, donc l'affirmation 2 est vraie.
• Choisir un nombre entier positif : 8
• Ajouter 1 : \(8+1=9\)
• Calculer le carré du résultat obtenu \(9^{2}=81\)
• Enlever le carré du nombre de départ. \(81-8^{2}=81-64=17\)
Dans ce cas, l'affirmation 1 est vraie (17 se termine par 7) ainsi que l'affirmation 2 (17 est bien égal au nombre de départ 8 auquel on ajoute le nombre entier qui le suit 9).
Lorsque le nombre de départ est 13 :
• Choisir un nombre entier positif : 13
• Ajouter 1 : \(13+1=14\)
• Calculer le carré du résultat obtenu \(14^{2}=196\)
• Enlever le carré du nombre de départ. \(196-13^{2}=196-169=27\)
Dans ce cas, l'affirmation 1 est vraie (27 se termine par 7) ainsi que l'affirmation 2 (27 est bien égal au nombre de départ 13 auquel on ajoute le nombre entier qui le suit 14).
b) Si on appelle \(x\) le nombre de départ :
• Choisir un nombre entier positif : \(x\)
• Ajouter 1 : \(x+1\)
• Calculer le carré du résultat obtenu \((x+1)^{2}\)
• Enlever le carré du nombre de départ. \((x+1)^{2}-x^{2}=(x+1+x)(x+1-x)=2x+1\)
Lorsque le nombre de départ est \(x\), le résultat obtenu est \(2x+1\).
Concernant l'affirmation 1, elle est fausse : prenons par exemple 4 comme nombre de départ, on obtient :
\(2x+1=2\times 4+1=9\) qui ne se termine pas par 7.
Concernant l'affirmation 2, lorsqu'on additionne deux nombres consécutifs, le résutat obtenu est :
\(x+(x+1)=2x+1\)
ce qui est le résultat obtenu, donc l'affirmation 2 est vraie.
Exercice 3 (6 points)
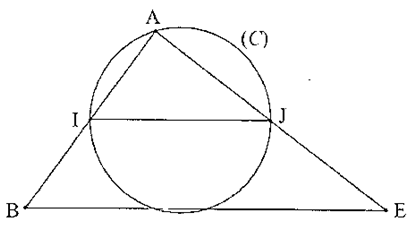
1) Dans le triangle ABE, I est le milieu de [AB] et J le milieu de [AE] donc d'après le théorème de la droite des milieux, les droites (IJ) et (BE) sont parallèles.
2) BE est la longueur la plus importante du triangle ABE. Nous avons :
\[\begin{align*} &AB^{2}+AE^{2}=6^{2}+8^{2}=36+64=100\\
&BE^{2}=10^{2}=100 \end{align*}\] Comme \(AB^{2}+AE^{2}=BE^{2}\), le triangle ABE est rectangle en A d'après la réciproque du théorème de Pythagore.
3) Le triangle AEB est rectangle en A, on peut utiliser les formules trigonométriques pour déterminer la mesure de l'angle \(\widehat{AEB}\) :
\[ \begin{align*} \cos{\widehat{AEB}}&=\frac{\text{côté adjacent à }\widehat{AEB}}{\text{hypoténuse}}\\ &=\frac{AE}{EB}\\ &=\frac{8}{10}\\ &=0.8 \end{align*} \] D'après la calculatrice, \(cos^{-1}(0.8)\approx 37^{\circ}\) donc l'angle \(\widehat{AEB}\) mesure approximativement 37° (valeur arrondie au degré près).
4)
a) Le triangle
IAJ est rectangle en A et inscrit dans le cercle (C), par conséquent
[IJ] est un diamètre de ce cercle. On en déduit que le centre
du cercle (C) est le milieu du segment
[IJ].
b) Nous devons calculer la longueur IJ. D'après la question 1, les droites (IJ) et (BE) sont parallèles donc d'après le théorème de Thalès, nous avons :
\[\begin{align*} &\frac{AI}{AB}=\frac{AJ}{AE}=\frac{IJ}{BE}\\ &\frac{3}{6}=\frac{4}{8}=\frac{IJ}{10} \end{align*}\] On en déduit la longueur IJ :
\[\begin{align*} &0.5=\frac{IJ}{10}\\ &IJ=0.5\times 10\\ &IJ=5\text{ cm} \end{align*}\] IJ mesure 5 cm.
Par conséquent, le rayon du cercle (C) mesure 2.5 cm.
b) Nous devons calculer la longueur IJ. D'après la question 1, les droites (IJ) et (BE) sont parallèles donc d'après le théorème de Thalès, nous avons :
\[\begin{align*} &\frac{AI}{AB}=\frac{AJ}{AE}=\frac{IJ}{BE}\\ &\frac{3}{6}=\frac{4}{8}=\frac{IJ}{10} \end{align*}\] On en déduit la longueur IJ :
\[\begin{align*} &0.5=\frac{IJ}{10}\\ &IJ=0.5\times 10\\ &IJ=5\text{ cm} \end{align*}\] IJ mesure 5 cm.
Par conséquent, le rayon du cercle (C) mesure 2.5 cm.
Exercice 4 (7 points)
| Nom du sportif | Alix | David | Gwenn | Yassin | Zoé |
| Distance parcourue (en km) | 35 | 42 | 27 | 35 | 42 |
| Durée de la randonnée | 2 h | 3 h | 1 h 30 min | 1 h 45 min | 1 h 36 min |
| Vitesse moyenne (en km/h) | 17,5 |
1) David a parcouru 42 kilomètres.
2) Pour David, la vitesse moyenne est égale à :
\[v=\frac{d}{t}=\frac{42}{3}=14\text{ km/h}\] Gwenn a mis 1 h 30 min pour effectuer un trajet de 27 km, soit une durée de 1.5 heure. Sa vitesse moyenne est donc égale à :
\[v=\frac{d}{t}=\frac{27}{1.5}=18\text{ km/h}\]
3)
| A | B | C | D | E | F | |
| 1 | Nom du sportif | Alix | David | Gwenn | Yassin | Zoé |
| 2 | Distance parcourue (en km) | 35 | 42 | 27 | 35 | 42 |
| 3 | Durée de la randonnée | 2 | 3 | 1.5 | ||
| 4 | Vitesse moyenne (en km/h) | 17,5 |
a) Transformons 1 h 45 min en heure(s) :
\[ \begin{align*} 1 \text{ heure }45\text{ minutes}&=1+\frac{45}{60}\text{ heure}\\ &=1.75\text{ heure} \end{align*} \] En E3, Il faut écrire 1.75.
b) Transformons 1 h 36 minutes en heure(s) :
\[ \begin{align*} 1 \text{ heure }36\text{ minutes}&=1+\frac{36}{60}\text{ heure}\\ &=1.6\text{ heure} \end{align*} \] En F3, il faut écrire 1.6.
c) Comme nous avons la relation suivante :
\[v=\frac{d}{t}\] Il faut saisir la formule suivante en B4 : B2/B3
4) Nous cherchons à connaître la durée de la randonnée :
\[\begin{align*} &v=\frac{d}{t}\\ &t=\frac{d}{v}\\ &t=\frac{35}{25}\\ &t=1.4\text{ heure}\\ &t=1\text{ heure}+0.4\times 60\text{ minutes}\\ &t=1\text{ heure }24\text{ minutes} \end{align*}\] Il a mis 1 h 24 min pour effectuer sa randonnée.
Exercice 5 (4 points)
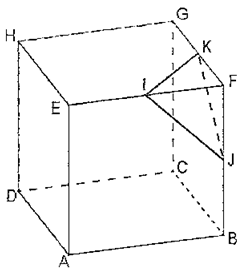
I est le milieu de [EF] et K le milieu de [FG], donc IF = FK = 3 cm.
Les faces d'un cube sont des carrés donc les (IF) est perpendiculaire à (FK).
Par conséquent, le triangle IFK est isocèle rectangle en F :

2) Les triangles FIK, FIJ et et FJK sont semblables ; ils sont tous isocèles (longueur = 3 cm) et rectangles en F, ce qui élimine le schéma 4 (seulement deux angles droits au lieu de trois).
Comme ces trois triangles sont semblables, nous avons nécessairement IJ = IK = JK donc le triangle IJK est équilatéral. Seul le schéma 3 parmi les schémas restants contient un triangle équilatéral, donc le bon patron est le schéma n°3.
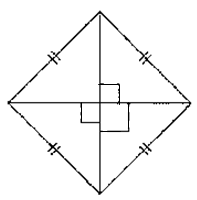 Schéma 1 |
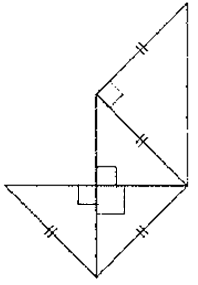 Schéma 2 |
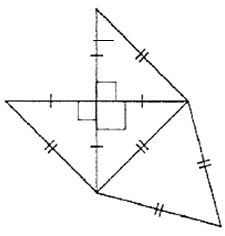 Schéma 3 |
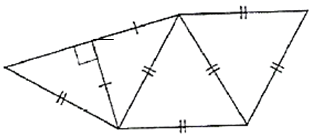 Schéma 4 |
3) Calcul du volume de la pyramide FIJK.
\[\begin{align*} V_{FIJK}&= \frac{\text{Aire d'une base}\times \text{hauteur}}{3}\\ &=\frac{\frac{FI\times FK}{2}\times FJ}{3}\\ &=\frac{\frac{3\times 3}{2}\times 3}{3}\\ &=4.5\text{ cm}^{3} \end{align*}\] Le volume de la pyramide est de 4.5 cm3.
Exercice 6 (4 points)
Modèle
PRIMA |
Version
ESSENCE Consommation moyenne : 6,2 L pour 100 km Type de moteur : essence Carburant : SP 95 Prix d'achat : 21 550 € |
VERSION
DIESEL Consommation moyenne : 5,2 L pour 100 km Type de moteur : diesel Carburant : gazole Prix d'achat : 23 950€ |
|
Estimation du prix
des carburants par
• Prix d’un litre de SP 95 : 1,415€M. Durand en 2015 • Prix d’un litre de gazole : 1,224€ |
1) Consommation annuelle de carburant en diesel :
\[22300\times\frac{5.2}{100}=1159.6\text{ litres}\] Budget carburant :
\[1159.6\times 1.224 \approx 1419.35€\]
| Version ESSENCE | Version DIESEL | |
| Consommation de carburant (en L) | 1 383 | 1 159.6 |
| Budget de carburant (en €) | 1 957 | 1 419.35 |
2) L'économie annuelle de carburant est égale à :
\[1957-1419.35=537.65€\] La différence de prix d'achat est égale à :
\[23950-21550=2400€\] Il rentabilisera l'investissement dans le véhicule diesel au bout de :
\[ \frac{2400}{537.65}\approx 4.46 \text{ années}\] Il faudra environ 4.5 ans pour compenser la différence de prix entre les deux versions.
Exercice 7 (3 points)
1) Surface occupée par les océans :\[1-\frac{5}{17}=\frac{12}{17}\] L'Océan Pacifique recouvre la moitié de cette superficie, soit :
\[\frac{12}{17}\times\frac{1}{2}=\frac{6}{17}\] L'Océan Pacifique recouvre 6/17 de la superficie totale de la Terre.
2) On peut remplir un tableau de proportionnalité :
| Fraction | Superficie |
| \(\frac{6}{17}\) |
180 000 000 |
| 1 |
\(x\) |
\[ \begin{align*} x&=\frac{180000000}{\frac{6}{17}}\\ &=180000000\times \frac{17}{6}\\ &=510000000 \end{align*} \] La superficie de la Terre est de 510 000 000 km2.