FRANCE SEPTEMBRE 2016 Correction du brevet

Exercice 1 (3 points)

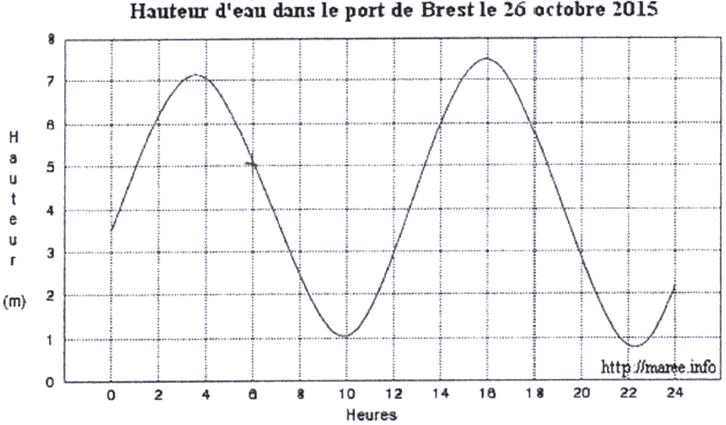
1)

2) Calcul du coefficient de cette marée :
\[C=\frac{7.4-4.2}{3.1}\times 100\approx 103\] Le coefficient de cette marée était approximativement de 103 (valeur arrondie à l'unité).

Exercice 2 (6 points)

1) Dans le triangle IKJ, le côté le plus long est [IJ]. Nous avons :
\[\begin{align*} IK^{2}+KJ^{2}&=3.2^{2}+2.4^{2}\\ &=10.24+5.76\\ &=16\\ & \\ IJ^{2}&=4^{2}\\ &=16 \end{align*}\] Nous remarquons que \(IK^{2}+KJ^{2}=IJ^{2}\) donc d'après la réciproque du théorème de Pythagore, le triangle IKJ est rectangle en K.

2) D'après la figure, le triangle ILM est rectangle en L, donc les droites (IL) et (LM) sont perpendiculaires.
Nous avons montré à la question précédente que le triangle IKJ est rectangle en K donc les droites (IL) et (KJ) sont perpendiculaires.
Les droites (KJ) et (LM) sont perpendiculaires à la même droite (IL) donc (KJ) et (LM) sont parallèles. On peut donc utiliser le théorème de Thalès :
\[ \frac{IK}{IL}=\frac{IJ}{IM}=\frac{JK}{LM}\] Nous connaissons IK, IL (= IK + KL), IJ et JK. Nous pouvons déterminer LM à partir des rapports suivants :
\[\begin{align*} &\frac{IK}{IL}=\frac{JK}{LM}\\ &\frac{IK}{IK+KL}=\frac{JK}{LM}\\ &\frac{3.2}{3.2+1.8}=\frac{2.4}{LM}\\ &\frac{3.2}{5}=\frac{2.4}{LM}\\ &LM=\frac{2.4\times 5}{3.2}\\ &LM=3.75\text{ mètres} \end{align*}\] LM mesure 3.75 mètres.

3) Le triangle KLM est rectangle en L donc d'après le théorème de Pythagore :
\[\begin{align*} &KL^{2}+LM^{2}=KM^{2}\\ &KM^{2}=1.8^{2}+3.75^{2}\\ &KM^{2}=3.24+14.0625\\ &KM^{2}=17.3025\\ &KM=\sqrt{17.3025}\\ &KM\approx 4.16\text{ mètres} \end{align*}\] KM mesure approximativement 4.16 mètres (valeur arrondie au centimètre près).

Exercice 3 (5,5 points)

1) En B15, la formule à saisir est :
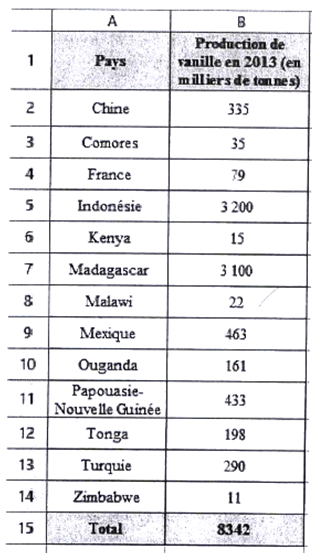
=SOMME(B2:B14)

2) Production mondiale de vanille par l'Indonésie et Madagascar :
3200 + 3100 = 6300
Part de la production de ces deux pays dans la production mondiale :
\[\frac{6300}{8342}\approx 0.755 \approx 76\%\] L'Indonésie et Madagascar produisent bien plus des trois quarts de la production mondiale de vanille.

3) Les cinq pays ayant produit le moins de vanille en 2013 sont : le Zimbabwe, le Kenya, le Malawi, les Comores et la France. La quantité de vanille produite par ces cinq pays est égale à :
 11 + 15 + 22 + 35 + 79 = 162
Part de la production de ces cinq pays dans la production mondiale :
\[\frac{162}{8342}\approx 0.019 \approx 2\%\] Ces 5 pays représentent environ 2% de la production mondiale de vanille (valeur arrondie à l'unité).

Exercice 4 (4,5 points)

1) Réponse c.
Pour l'inéquation a), 2 ne peut pas être solution.
Pour l'inéquation b) : \(-4\times2-3=-8-3=-11<-10\) donc 2 n'est pas solution de cette inéquation.
Pour l'inéquation c) : \(5\times2-4=10-4=6\leq7\) donc 2 est une solution de cette inéquation.
Pour l'inéquation d) : \(8-3\times2=8-6=2<3\) donc 2 n'est pas solution de cette inéquation.

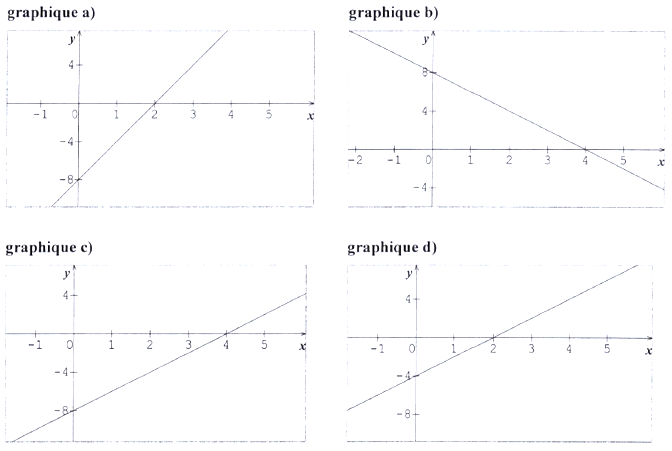
2) Réponse c.
Le coefficient directeur (égal à 2) est positif donc la pente de la droite est positive, ce qui élimine le graphique b.
L'ordonnée à l'origine vaut -8, donc lorsque \(x\) vaut 0, \(y\) vaut -8, ce qui élimine le graphique d.
Il reste les graphiques a et c.
Calculons \(f(2)\) par exemple :
\[f(2)=2\times2-8=4-8=-4\] donc l'image de 2 par la fonction \(f\) est -4. C'est le cas pour le graphique c mais pas pour le graphique a. La bonne réponse est le graphique c.

3) Réponse b.
100 mètres en 10 secondes, cela fait 600 mètres en 60 secondes (1 minute), et donc 36 000 mètres en 60 minutes (1 heure), soit 36 km/h.

Exercice 5 (5 points)

1) Figure

2) "Tracer le cercle de centre J et de rayon [CJ]".

3) Les angles inscrits\(\widehat{EGI}\) et \(\widehat{EHI}\) interceptent le même arc de cercle \(\overset{\frown}{EI}\) donc ils ont nécessairement la même mesure : \(\widehat{EGI}=\widehat{EHI}\).
Ceci est le cas pour tous les pentagrammes construits avec cette méthode.

Exercice 6 (7 points)

Document 1 : Informations sur la véranda


Document 2 : informations sur les tuiles

Modèle	Tuile romane	Tuile régence
Coloris	"littoral"	"Brun vieilli"
Image
Quantité au m2	13	19
Poids au m2 (en kg)	44	44
Pente minimale pour permettre la pose	15°	18°
Prix à l'unité	1€79	1€24
Prix au m2	23,27€	??? €

1) Chaque tuile coûte 1€24 et il en faut 19 pour couvrir un mètre carré. Par conséquent, le prix au m² des « tuiles régence » est égal à :
\[1.24\times 19=23.56\] Le prix au m² des « tuiles régence » est de 23€56.

2) Calcul de la longueur CD :
CD = BD - BC = 3.10 - 2.10 = 1
CD mesure 1 mètre.
Le triangle CDE est rectangle en C donc on peut utiliser les formules trigonométriques pour déterminer la mesure de l’angle \(\widehat{DEC}\) :
\[ \begin{align*} \tan\widehat{DEC}&=\frac{\text{côté opposé à } \widehat{DEC}}{\text{côté adjacent à } \widehat{DEC}}\\ &=\frac{CD}{CE}\\ &=\frac{1}{2.85} \end{align*} \] D'après la calculatrice :
\[\tan^{-1}\left(\frac{1}{2.85}\right)\approx 19.33^{\circ}\] La pente du toît est approximativement de 19.33°, les deux modèles peuvent donc être posés puisqu'il faut au moins 15° pour le modèle "romane" et 18° pour le modèle "régence".

3) La surface à couvrir est le rectangle EFGD. Pour calculer sa surface, il nous manque la longueur ED. Or on sait que le triangle EDC est rectangle en C donc d'après le théorème de Pythagore, nous avons :
\[\begin{align*} &CD^{2}+CE^{2}=DE^{2}\\ &DE^{2}=1^{2}+2.85^{2}\\ &DE^{2}=1+8.1225\\ &DE^{2}=9.1225\\ &DE=\sqrt{9.1225} \text{ m (valeur exacte)} \end{align*}\] Nous pouvons calculer la surface du rectangle EFGD :
\[\begin{align*} A_{EFGD}&=ED\times EF\\ &=\sqrt{9.1225}\times 6.10\\ &\approx 18.43 \text{ m}^{2} \end{align*}\] (Valeur arrondie au dm² supérieur).
Il faut ensuite augmenter cette surface de 5%. La surface à commander est donc de :
\[S=\left(1+\frac{5}{100}\right)\times 18.43=19.3515\text{ m}^{2}\] Sachant qu'il en faut 13 au m², le nombre de tuiles romanes qu'elle devra comander est égal à :
\[19.3515\times 13=251.2695\Rightarrow 252\] Elle devra commander 252 tuiles.

Exercice 7 (5 points)

1) Si \(x\) est le prix d'une pizza ronde, alors le prix d'une pizza carrée est \(x+1\). Sachant que Pierre a payé 14,20€ pour une pizza ronde et une pizza carrée, nous avons :
\[\begin{align*} &x+(x+1)=14.20\\ &2x+1=14.20\\ &2x=14.20-1\\ &2x=13.20\\ &x=\frac{13.20}{2}\\ &x=6.60 \end{align*}\] Une pizza ronde coûte 6€60 tandis qu'une pizza carrée coûte 7€60.

2) Etant donné que les pizzas ont la même épaisseur, il faut comparer les surfaces de chaque part.
La pizza ronde a un diamètre de 34 cm, soit un rayon de 17 cm. La pizza ronde est composée de 8 parts donc la surface de chaque part est égale à :
\[\begin{align*} S_{\text{part pizza ronde}}&=\frac{1}{8}\times\pi\times r^{2}\\ &=\frac{1}{8}\pi\times 17^{2}\\ &\approx 113.49\text{ cm}^{2} \end{align*}\] La surface de chaque part de la pizza ronde est approximativement égale à 113.49 cm².
La pizza carrée a ses côtés de longueur 34 cm . Elle est composée de 9 parts donc la surface de chaque part est égale à :
\[\begin{align*} S_{\text{part pizza carrée}}&=\frac{1}{9}\times c^{2}\\ &=\frac{1}{9}\times 34^{2}\\ &\approx 128.44\text{ cm}^{2} \end{align*}\] La surface de chaque part de la pizza carrée est approximativement égale à 128.44 cm².
Par conséquent, on trouve les plus grandes parts dans la pizza carrée.

Correction du brevet de mathématiques France Métropole - La Réunion - Antilles - Guyane 16 septembre 2016 (3ème)
© Planète Maths