GEOMETRIE DANS L'ESPACE, VOLUMES
|
Exercice 1
L'aquarium suivant est une sphère de centre A et de rayon 20 cm à laquelle on a enlevé une partie appelée "calotte sphérique". Cette sphère est en effet coupée par un plan tel que AB = 7 cm. Le point C appartient à la sphère et au plan.
1) Quelle est la hauteur de l'aquarium ?
2) Quelle est la nature de la section de cet aquarium par le plan ?
3) Sachant que le triangle ABC est rectangle en B, quelle est le rayon d'ouverture de l'aquarium (la distance BC) ? Donner le résultat sous forme exacte puis approchée au mm près.
4) Calculer le volume de l'aquarium sachant que celui de la calotte sphérique est égal à :
\[ \frac{7943}{3}\pi \text{ cm}^{3} \] 5) Combien de litres d'eau faut-il pour le remplir au maximum ?
Exercice 2
Soit la pyramide EABCD de base rectangulaire ABCD et de hauteur AE. On donne :AE = 10 cm ; AB = 3 cm ; BC = 6 cm.
La pyramide EABCD est coupée par un plan parallèle à sa base au point F tel que AF = 4 cm.

1) Quelle est la nature de la section de la pyramide EABCD par la plan parallèle à sa base ABCD et passant par F ?
2) Calculer la longueur FG.
3) La longueur FG est une réduction de la longueur AB : quelle est la valeur du coefficient de réduction ?
4) Calculer l'aire de la base ABCD. A partir du résultat de la question 3, déduire l'aire du quadrilatère FGHI.
5) Calculer le volume de la pyramide EABCD. A partir du résultat de la question 3, déduire celui de la pyramide EFGHI.
Exercice 3
Cet exercice se propose de calculer le volume d'un cône tronqué.Soit un cône dont la base est un cercle de rayon AE = 3 cm et de hauteur AC = 6 cm. On réalise la section de ce cône par un plan parallèle à sa base et passant par le point B tel que AB = 3 cm.

2) Calculer la longueur BD.
3) La longueur BD étant une réduction de la longueur AE, quelle est la valeur du coefficient de réduction ?
4) Calculer l'aire du cercle de rayon AE. En déduire l'aire du cercle de rayon BD en utilisant le résultat de la question précedente.
5) Quel est le volume du grand cône ? En déduire celui du cône de base circulaire de rayon [BD] à partir du résultat de la question 3.
6) Quel est le volume du cône tronqué, c'est à dire du solide ayant pour base inférieure le cercle de rayon [AE] et pour base supérieure le cercle de rayon [BD] ?
Exercice 4
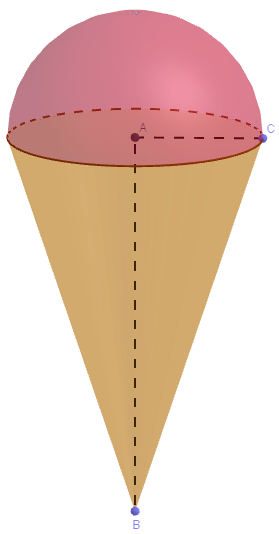
Un cornet de glace est composé d'un cône surmonté d'une demi-boule. Sur le dessin ci-dessous, on donne :AB = 13 cm ; AC = 2,5 cm.
On suppose que le cône est entièrement rempli de glace.